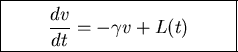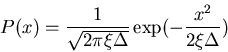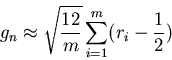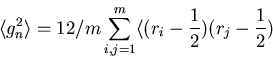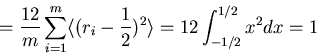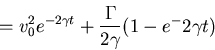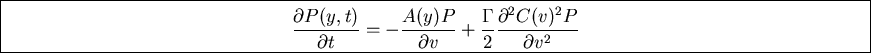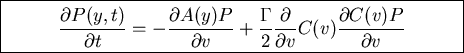

Next: About this document ...
9. Langevin approach
LAST TIME:
- We discussed transformations of
the Fokker-Planck equation.
- One of these eliminated an heterogeneous
diffusion term.
- We discussed in detail an example of
variable diffusion constant.
- Heteregeneous diffusion produced net effective
drift
 motor!
motor!
Today try a different approach.
Master equation approach considered time evolution of probability distribution.
Fokker-Planck equation was derived from master equation typically from system size
expansion.
LANGEVIN EQUATION stochastic d.e.
Simplest case: BROWNIAN MOTION.
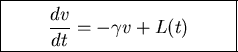
v= velocity of Brownian particle.
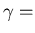 friction term.
friction term. L(t)= noise term.
L(t)= noise term.
Collisions with other molecules gives rise
to
average force (friction)
+random force
Require:
if
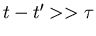 time between molcular collisions require
time between molcular collisions require
M= mass of Brownian particle.
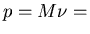 random part of impulse transmitted at collision.
random part of impulse transmitted at collision.
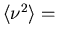 variance of
variance of 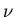 .
.
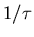 collision rate
collision rate
Let
x stochastic variable.
By central limit theorem
of statistics, x characterized by Gaussian
probability distribution
where
Physically, Langevin equation corresponds to limit
Mathematically L(t) realization of Wiener process
Langevin equation suitable for computer simulations!
Discretize time
where gn picked from Gaussian distribution with variance
1 and
Random number generators typically generate uniformly
distributed numbers in range
0<r<1.
Simple
method to generate
Gaussian distribution is
to make use of results from Brownian motion!
Clearly
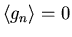 and we find
and we find
We next generalize to take the limit 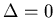 and
write the Langevin equation on the form
and
write the Langevin equation on the form
where
and
with 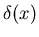 the Dirac
the Dirac 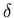 -function.
-function.
Noise with these properties called white.
For Gaussian process higher moments given by e.g.
Can formally solve Langevin equation with initial condition
v=v0 for t=0
Find
Restrict t to small value 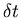 .
.
The speed will then change by small amount 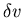
Get jump moments
Higher order jump moments of higher order in 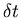 .
.
Find that Langevin equation equivalent
to Fokker-Planck (Rayleigh) equation
Easy to generalize to case of nonlinear "force" with additive
noise e.g.
assume as before
Can calculate jump moments and find Langevin
equation equivalent to Fokker-Planck equation
What about nonlinear noise?
Trouble is expression is ambiguous!
L is a
process
with discrete jumps.
Should C(v) be evaluated using
value of v before or after jump?
Or, should an average
value be chosen?
Choice matters! (We saw last time that
heterogeneous diffusion gives rise to effective drift term.)
If noise internal:
E.g. birth and death processes
"Natural" to say that rate of processes should be calculated
before process happens.
Ito
interpretation:
Can show by calculating jump moments that result is
Fokker-Planck equation on form
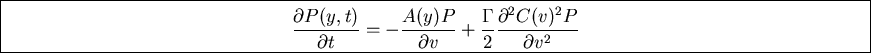
If noise external
Open system.
Must consider
that no noise is truly white!
There is always a nonzero
relaxation time.
"Natural" to evaluate C(v) for
average value of v during process.
Stratanovich interpretation
Get Fokker-Planck equation on form
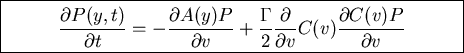
SUMMARY
- Langevin approach gives rise to stochastic
differential equation.
- For additive white Gaussian noise Langevin equation
equivalent to Fokker-Planck
equation.
- When noise nonlinear need to impose interpretation.
- Ito and Stratanovich interpretation most common.
- No real mathematical difficulty. Can transform
equation with Ito interpretation into one with
Stratanovich interpretation or vice versa.
- Difficulty with physics. Which formula gives
the correct result? Need to go back to master equation
and look at microscopic processes.
Click here for Return to title page
Click here for 10 Molecular motors


Next: About this document ...
Birger Bergersen
1998-10-14