

Next: About this document ...
8. Transformations and blow torches
LAST TIME:
- Discussed absorbing boundary conditions.
- Artificial boundary
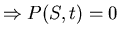 on boundary S
on boundary S
- Natural boundaries
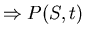 "well behaved".
"well behaved".
- Examples: Diffusion near "cliff". Genetic drift.
- Derived Kramers' escape rate:
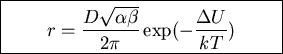
where
HETEROGENEOUS DIFFUSION
Consider Fokker-Planck equation on form
Coordinate transformation
a(y)=A(x);b(y)=B(x)
Using
we find
Choose transformation
where lower limit of integral is arbitrary.
Get Fokker-Planck equation on form
where we have a new "effective" force
Problem with state dependent diffusion
has been transformed into problem
with constant diffusion but new
drift term.
Physical example: Thermoelectric effect!
Example
PERIODIC FORCE AND TEMPERATURE
Fokker-Planck equation
Coordinate transformation:
Choose 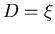
Effective force
The associated potential is
We are interested in the case 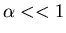
For small 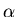 the potential has minima at
the potential has minima at
The maxima occur at
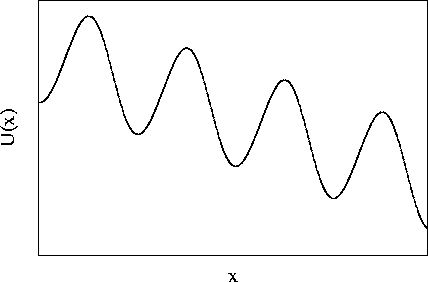
The potential difference when a particle
jumps over a barrier to the left or right is
The Kramers escape rates are then
The net velocity of a particle in
the potential is thus
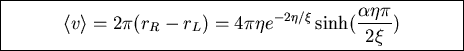
BLOWTORCHES
The previous example is an illustration of
Landauer's blowtorch paradox.
The Kramers' escape rate formula depends only on the
behavior of the potential near maxima and minima.
This interpretation can be misleading!
Blowtorch applied to "irrelevant" part of path
effectively lowers potential maximum.
Some people believe similar considerations
apply to markets.
Sometimes seemingly "irrelevant"
events affects volatility!
Such events called "sunspots".
SUNSPOTS MATTER!
TRANSFORMATION TO SCHRÖDINGER EQUATION
Fokker-Planck equation generally not
self-adjoint.
Eigenfunctions associated with reflecting or
absorbing boundaries need not be orthogonal.
Consider Fokker-Planck equation
Introduce new variable 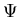
where
Find that 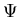 satisfies Schrödinger type
equation
satisfies Schrödinger type
equation
with the expression inside the square bracket
playing the role of a potential.
SUMMARY
- We have introduced two useful transformation of
the Fokker-Planck equation.
- The first transformation eliminates a
heterogeneous diffusion term.
- The second transformation changes the Fokker-Planck
equation into a self-adjoint Schrödinger type equation.
- We have discussed in detail and example of
variable diffusion constant.
- The result of discussion resolved the
Blowtorch paradox.
Click here for 9.Langevin approach
Click here for Return to title page


Next: About this document ...
Birger Bergersen
1998-10-07
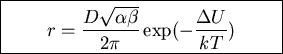
![\begin{displaymath}\frac{\partial P(x,t)}{\partial t}=-\frac{\partial}{\partial ...
...)P(x,t)-\frac{1}{2}\frac{\partial}{\partial x}B(x)P(x,t)\right]\end{displaymath}](img7.gif)
![\begin{displaymath}\frac{\partial\Pi(y,t)}{\partial t}=-\frac{\partial}{\partial...
...-\frac{y'}{2}\frac{\partial}{\partial y}b(y)y'\Pi(y,t)
\right]\end{displaymath}](img10.gif)
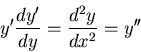
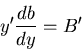
![\begin{displaymath}\frac{\partial\Pi}{\partial t}=-\frac{\partial}{\partial y}
...
...']\Pi(y,t)+\frac{1}{2}(y')^2b\frac{\partial^2\Pi}{\partial y^2}\end{displaymath}](img13.gif)
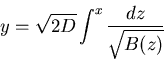
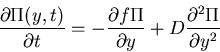
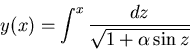
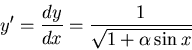
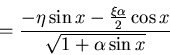
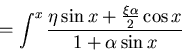
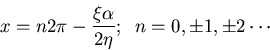
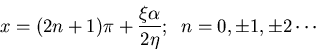

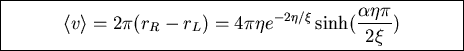
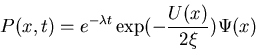
![\begin{displaymath}-\xi\frac{d^2\Psi}{dx^2}+\left[\frac{1}{4\xi}(\frac{dU}{dx})^2
-\frac{1}{2}\frac{d^2 U}{dx^2}\right]\Psi=\lambda\Psi\end{displaymath}](img44.gif)