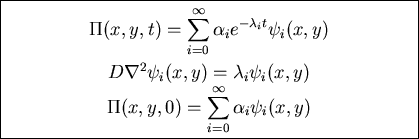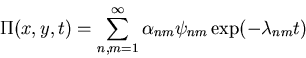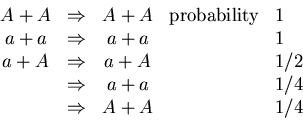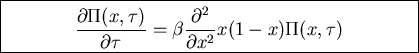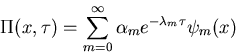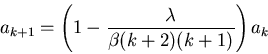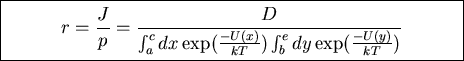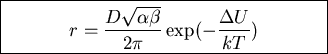

Next: About this document ...
7. Absorbing boundaries
LAST TIME
Tim Duty described branching processes e.g. birth
and death processes:
System of n objects of type A.
Elementary processes:
Discussed methods to calculate
survival probability and cascade size distribution.
State with no A- particles absorbing state.
Once in such a state system trapped and there is no escape!
Today want to discuss how to treat absorbing states in continuum limit.
LIMBO STATE and FICTITIOUS STATE
Master equation for one step processes:
If b(0)=0, call n=0 limbo state.
P*(t)=probability of limbo state.
If
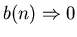 as
as
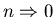 natural boundary.
natural boundary.
Otherwise n=0 artificial boundary.
In continuum limit must
avoid treating n=0 as separate case.
If
boundary artificial
introduce fictitious state n=0.
Boundary condition P(0,t)=0.
Normalization:
If
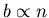 and
and
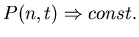 as
as
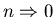 there is probability
current into limbo state!
there is probability
current into limbo state!
Example:
DIFFUSION NEAR A CLIFF
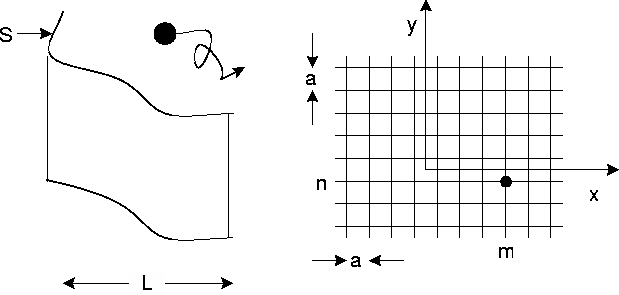
Jumps at rate 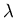 distance a in
distance a in
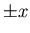 and
and 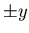 directions.
directions.
S absorbing boundary.
Master equation:
a "smallness parameter"
L= macroscopic length scale
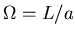 system size parameter
system size parameter
S= artificial boundary!
Diffusion equation:
where
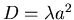
Boundary condition 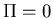 on
on
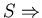 eigenvalue problem:
eigenvalue problem:
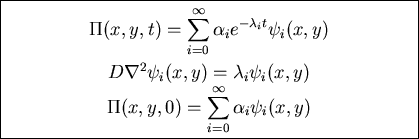
Example:
Square with corners at
(0,0),(0,L),(L,L),(L,0)
and absorbing sides
For long times smallest eigenvalue (ground state) dominates!
Asymptotic formula for survival probability
Example of problem with natural boundaries:
GENETIC DRIFT
A gene is expressed as allele a or A.
The allele is neutral: there is no competititve advantage
to being either A or a.
Stable population size: Population pairs off.
Each pair produces two offspring.
Only last two processes change composition of population. Rate of
contributing processes:
 size of population.
size of population.
n = number of individuals of type a.
Master equation:
Macroscopic variables
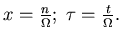
Fokker-Planck equation
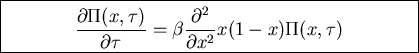
Initial condition
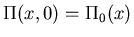 .
.
Try solution on form
Differential equation singular at x=0,x=1! Cannot impose
arbitrary boundary condition.
Require that eigenfunctions well behaved at
x=0,x=1. Try
Get
Radius of convergence of power series
x=1. For solution to be well behaved at x=1
require that series breaks off! Eigenvalues:
Lowest eigenvalue
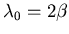 .
Asymptotically, probability that both alleles
can be found in population decays as
.
Asymptotically, probability that both alleles
can be found in population decays as
Note that lifetime
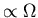 ,
population size!
,
population size!
Equation for 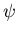 special case of hypergeometric
equation. General solution can be expressed in terms
of Gegenbauer polynomials!
For details see Kimura [1955]
special case of hypergeometric
equation. General solution can be expressed in terms
of Gegenbauer polynomials!
For details see Kimura [1955]
KRAMERS ESCAPE RATE
Consider an overdamped partice moving in a potential
well near a "cliff".
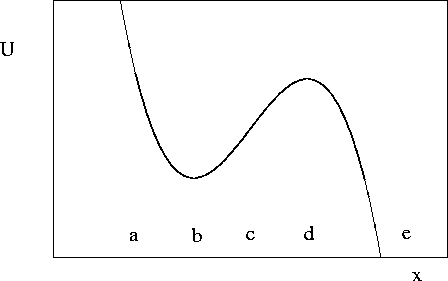
Force
- Assume
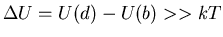
Metastable state "quasi-stationary"
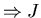 approximately independent of x.
approximately independent of x.
- Assume particle reaching C are "lost".
Impose absorbing boundary conditions at e.
Fokker-Planck equation
Probability current
Integrate from b to e with P(e,t)=0
Assume that near b
Probability that particle is "near" b
Escape rate
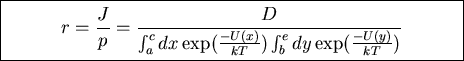
The integrals in the boxed expression above
can be evaluated numerically to arbitrary accuracy.
In order to get a simple and easy to remember expression we
note that the dominant contribution from first integral
comes from near minimum. Expand near b
Second integral dominated by contribution
from near maximum
Get Kramers' escape rate
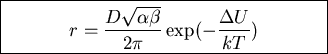
This is an asymptotic formula valid in the limit
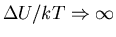 .
See the book of Risken for low order correction terms!
.
See the book of Risken for low order correction terms!
SUMMARY
- Discussed absorbing boundary conditions for
- artificial boundaries
- natural boundaries.
- Discussed diffusion near a "cliff".
- Solved a genetic drift problem.
- Derived Kramers formula for escape rate
from metastable state
Click here for Return to title page
Click here for 8. Transformations and blow torches


Next: About this document ...
Birger Bergersen
1998-10-03
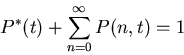

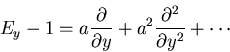
![\begin{displaymath}\frac{\partial\Pi(x,y,t)}{\partial t}=D\left[\frac{\partial^2}{\partial x^2}+
\frac{\partial^2}{\partial y^2}\right]\Pi\end{displaymath}](img21.gif)