

Next: About this document ...
4. Brownian particles
LAST TIME
Started to discuss Fokker-Planck equations on the form
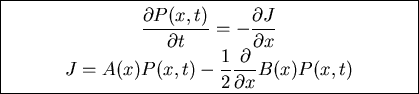
J=Probabiliy current
A(x)P(x,t)=drift term or transport term
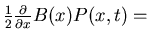 diffusion term
Linear
diffusion term
Linear
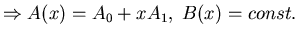
Ornstein-Uhlenbeck process
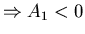
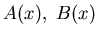 obtained from jump moments
obtained from jump moments
Today: Examples
MESOSCOPIC PARTICLE IN STATIONARY FLUID
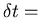 "infinitesimal" time
"infinitesimal" time
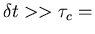 mean time for collisions
mean time for collisions
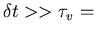 velocity relaxation time
velocity relaxation time
(see later)
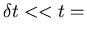 time of interest
time of interest
f=external force on particle
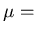 mobility
mobility
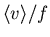
v= velocity
jump moments:
FOKKER-PLANCK EQUATION
![\fbox{\parbox{11cm}{
\begin{displaymath}\frac{\partial P(x,t)}{\partial t}=-\fr...
...x,t)]+\frac{1}{2}\frac{\partial^2}{\partial x^2}[a_2
P(x,t)]\end{displaymath}}}](img14.gif)
BROWNIAN MOTION
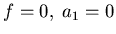
This is just the diffusion equation, hence require
Fokker-Planck equation does not admit a stationary (steady) state
but can find
![\fbox{\parbox{7cm}{
\begin{displaymath}P(x,t\vert,0)=\frac{\exp\left[-\frac{x^2}{4Dt}\right]}{\sqrt{4\pi Dt}}\end{displaymath}
}}](img18.gif)
Gaussian processes like the boxed expression are also called
Wiener processes
PARTICLE IN FIELD OF GRAVITY
We now have
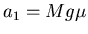 .
Presence of field changes a2 little
.
Presence of field changes a2 little
Why is this assumption reasonable?
The resulting Fokker-Planck equation is
No stationary solution for
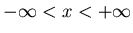 .
.
We can solve time dependent equation:
Go to moving frame
Left with diffusion equation for 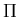 !
!
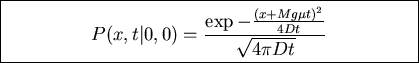
REFLECTING BOUNDARY
Steady state exists if
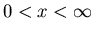 !
!
Vessel with diffusing particle has a bottom.
Require that probability current vanishes in steady state
with solution
At equilibrium must have
Get Einstein relation
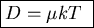
For time dependent problem apply zero current condition only at x=0!
RAYLEIGH PARTICLE
Consider fine time scale:
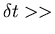 time between collisions
time between collisions
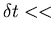 time for relaxation of velocity
time for relaxation of velocity
velocity v independent variable
Macroscopic law
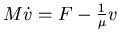
E.g. for spherical Stokes particle
r=radius, 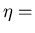 viscosity
viscosity
Jump moments
Assume
No external force!
Get Fokker Planck-equation
Stationary state (J(v)=0!)
with solution
Maxwell-Boltzmann distribution:
![\fbox{\parbox{9cm}{
\begin{displaymath}P_e(v)=\sqrt{\frac{M}{2\pi kT}}exp-\left[\frac{Mv^2}{kT}\right]\end{displaymath}
}}](img42.gif)
Comparing expressions we find
RAYLEIGH EQUATION
Equation is linear and describes an Ornstein-Uhlenbeck process. Solution:
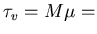 velocity relaxation time
velocity relaxation time
We have if
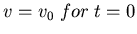
Can also calculate equilibrium velocity-velocity correlation
We find
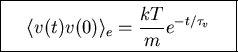
GENERALIZE TO ARBITRARY FORCE
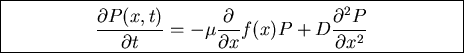
Overdamped motion in force field.
Macroscopic equation of motion Aristotelian:
not Newtonian.
Aristotle ok if
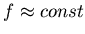 if
if
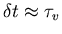
Substituting
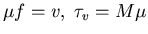 we find
for the boxed expression to be valid
we find
for the boxed expression to be valid
If condition
not satisfied both v and x
independent variables!
Jump moments
Fokker-Planck equation:
KRAMERS EQUATION
![\fbox{\parbox{12cm}{
\begin{displaymath}\frac{\partial P(x,v,t)}{\partial t}=-v...
...ial v}+\frac{kT}{M}\frac{\partial^2 P}{\partial v^2}\right]\end{displaymath}
}}](img62.gif)
SUMMARY
Click here for 5. Several variables, SIR-model
Click here for Return to title page


Next: About this document ...
Birger Bergersen
1998-10-03
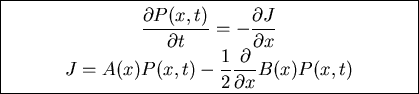
![\fbox{\parbox{11cm}{
\begin{displaymath}\frac{\partial P(x,t)}{\partial t}=-\fr...
...x,t)]+\frac{1}{2}\frac{\partial^2}{\partial x^2}[a_2
P(x,t)]\end{displaymath}}}](img14.gif)
![\fbox{\parbox{7cm}{
\begin{displaymath}P(x,t\vert,0)=\frac{\exp\left[-\frac{x^2}{4Dt}\right]}{\sqrt{4\pi Dt}}\end{displaymath}
}}](img18.gif)
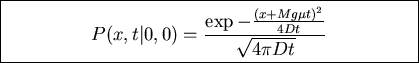
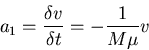
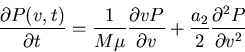
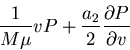
![\begin{displaymath}P_s(v)\propto \exp-\left[\frac{v^2}{a_2M\mu}\right]\end{displaymath}](img41.gif)
![\fbox{\parbox{9cm}{
\begin{displaymath}P_e(v)=\sqrt{\frac{M}{2\pi kT}}exp-\left[\frac{Mv^2}{kT}\right]\end{displaymath}
}}](img42.gif)
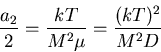
![\begin{displaymath}\frac{\partial P(v,t)}{\partial t}=\frac{1}{M\mu}\left[ \frac...
...partial v}+\frac{kT}{M}\frac{\partial^2 P}{\partial v^2}\right]\end{displaymath}](img44.gif)
![\begin{displaymath}P(v,t\vert v_o,0)=\frac{\exp-\left[\frac{
M(v-v_0e^{- t/\ta...
...tau_v})}\right]}
{\sqrt{\frac{2\pi kT}{M}(1-e^{-2 t/\tau_v})}}\end{displaymath}](img45.gif)
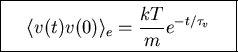
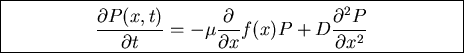
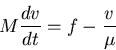
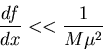
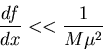
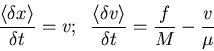
![\begin{displaymath}\frac{\langle (\delta x)^2\rangle}{\delta t}=v^2\delta t\appr...
... v\rangle}{\delta t}=v[\frac{\mu f -v} {M\mu}]\delta t\approx 0\end{displaymath}](img60.gif)
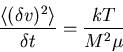
![\fbox{\parbox{12cm}{
\begin{displaymath}\frac{\partial P(x,v,t)}{\partial t}=-v...
...ial v}+\frac{kT}{M}\frac{\partial^2 P}{\partial v^2}\right]\end{displaymath}
}}](img62.gif)