

Next: About this document ...
3. Fokker Planck equation.
LAST TIME DISCUSSED
MALTHUS-VERHULST PROBLEM
Birthrate:
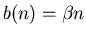
Death rate:
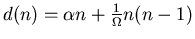
Made a system size expansion
Found that  satisfied a macroscopic rate equation
satisfied a macroscopic rate equation
If
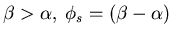 stable steady state
stable steady state
An initial fluctuation x0 evolved so that
FOKKER PLANCK EQUATION FOR
FLUCTUATIONS ABOUT MACROSCOPIC STEADY STATE
Find time independent distribution 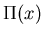 for long times
for long times
Get
Requirement that
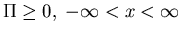 gives const=0
gives const=0
Normalization condition
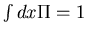 gives
gives
Gaussian distribution!
TIME EVOLUTION OF FLUCTUATIONS
Can also solve time dependent equation
All necessary information in
P(x,t|x0,0)
(Notation
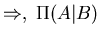 is the conditional probability for
A given B)
Can show (e.g. by Fourier methods)
is the conditional probability for
A given B)
Can show (e.g. by Fourier methods)
Probability distribution Gaussian with
evolving
variance and mean
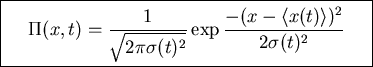
Variance and mean same as before
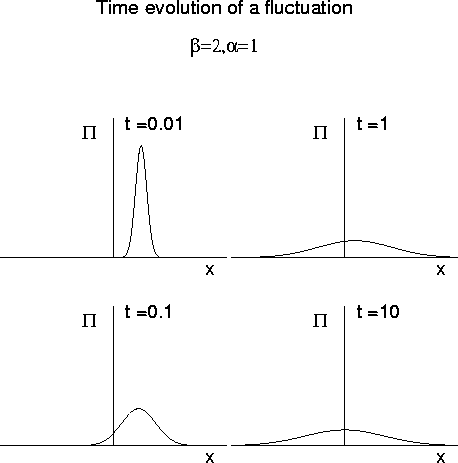
So far have argued only from an example
More general form of FOKKER-PLANCK equation
Also called Smoluchowski equation, or
second Kolmogorov equation.
Structure of equation:
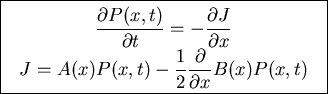
J=Probabiliy current
A(x)P(x,t)=drift term or transport term
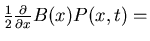 diffusion term
diffusion term
ANALOGY WITH
MACROSCOPIC CURRENTS
Suppose n(x)= concentration of conserved quantity e.g. particle number
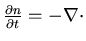 j
j
j= particle current
Current from constitutive relation e.g.
j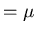 f
f
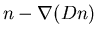
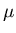 =mobility given by
=mobility given by
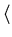 v
v
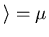 f
f
f=force on particles (e.g. mg or eE.)
D= diffusion constant
In Fokker-Planck equation deal with probability density rather than
particle density!
LINEAR PROCESSES
By definition
Fokker-Planck equation linear in P
Fokker-Planck equations commonly referred to
as linear if A(x) linear and
B(x)=const.
Stationary processes governed by linear Fokker Planck equation
called Ornstein-Uhlenbeck processes.
Stationarity requires A1<0.
Time dependent Fokker-Planck equation can be solved explicitly
for linear processes (Malthus-Verhulst problem example).
Many numerical methods available for nonlinear
processes!
STEADY STATE SOLUTION
(when exist)
can be found for arbitrary
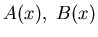
In steady state probability current is zero
for unbounded system
with solution
![\fbox{\parbox{7cm}{
\begin{displaymath}P_s(x)=\frac{const}{B(x)}\exp\left[2\int^x\frac{A(y)}{B(y)}dy\right]\end{displaymath}
}}](img33.gif)
PLANCK'S DERIVATION
Continuous version of master equation
Define r=q-q' and
w(q',r)=W(q|q')
Expand
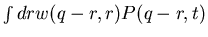 w.r.t. r in
first argument
w.r.t. r in
first argument
Next, define the jump moments
Get Fokker-Planck equation to 2nd order!
![\fbox{\parbox{9cm}{
\begin{displaymath}\frac{\partial P(q,t)}{\partial t}=-\fra...
...)]+\frac{1}{2}\frac{\partial^2}{\partial q^2}[a_2(q)
P(q,t)]\end{displaymath}}}](img40.gif)
ADDED BONUS OF DERIVATION:
Physical interpretation of
A(q), B(q) in terms of jump moments.
Why stop at second order?
Include all terms in expansion!
Kramers-Moyal expansion:
![\fbox{\parbox{8cm}{
\begin{displaymath}\frac{\partial P(q,t)}{\partial t}=\sum_...
...c{(-1)^n}{n!} \frac{\partial^n}{\partial q^n}[a_n(q)P(q,t)]\end{displaymath}
}}](img41.gif)
Pawula's theorem
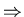 if break off at finite order beyond 2nd,
P(q,t) no longer positive
if break off at finite order beyond 2nd,
P(q,t) no longer positive
definite!
Expansion to all order
equivalent to master
equation.
System size expansion
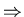 higher than 2nd order jump moments
higher order contributions in
higher than 2nd order jump moments
higher order contributions in
 (van Kampen).
(van Kampen).
SUMMARY
- Found steady state probability distribution in Malthus-Verhulst problem.
- Could also compute evolution of individual fluctuation.
- Considered a more general form of Fokker-Planck equation.
- Interpreted terms in equation in terms of probability current, drift and
diffusion.
- Defined linear Fokker-Planck equation as
describing Ornstein-Uhlenbeck process.
- Derived Fokker-Planck equation from jump moments.
- Showed that continuous master equation
equivalent to Kramers-Moyal expansion.
Click here for 4. Brownian particles
Click here for Return to title page


Next: About this document ...
Birger Bergersen
1998-09-18
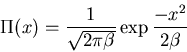
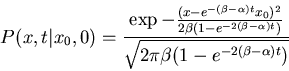
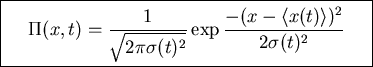

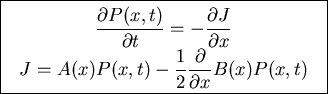
![\fbox{\parbox{7cm}{
\begin{displaymath}P_s(x)=\frac{const}{B(x)}\exp\left[2\int^x\frac{A(y)}{B(y)}dy\right]\end{displaymath}
}}](img33.gif)
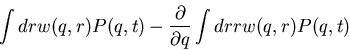
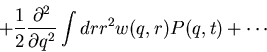
![\fbox{\parbox{9cm}{
\begin{displaymath}\frac{\partial P(q,t)}{\partial t}=-\fra...
...)]+\frac{1}{2}\frac{\partial^2}{\partial q^2}[a_2(q)
P(q,t)]\end{displaymath}}}](img40.gif)
![\fbox{\parbox{8cm}{
\begin{displaymath}\frac{\partial P(q,t)}{\partial t}=\sum_...
...c{(-1)^n}{n!} \frac{\partial^n}{\partial q^n}[a_n(q)P(q,t)]\end{displaymath}
}}](img41.gif)