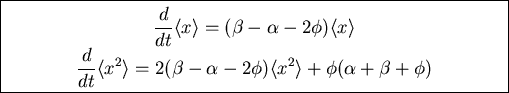

Next: About this document ...
2. System size expansion
LAST TIME:
Introduced the master equation
for discrete system:
For birth and death processes
d=death rate.
b=birth rate.
Macroscopic rate equation
Today: Want to study validity of
rate equation and fluctuations of
n for large system.
EXPANSION OF THE MASTER EQUATION
Expect for large systems:
Mean
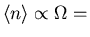 system size parameter.
system size parameter.
Fluctuations
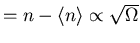 .
.
Describe this situation as
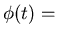 non-fluctuating variable.
non-fluctuating variable.
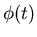 will satisfy
ordinary differential equation (normally just
rate equation).
will satisfy
ordinary differential equation (normally just
rate equation).
x fluctuating continuous variable with
probability distribution 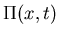 .
.
TRANSFORMATION OF VARIABLES
When n fluctuates by an amount 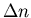 ,
x
will fluctuate by
,
x
will fluctuate by
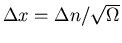 .
.
RAISING AND LOWERING OPERATORS
Ef(n)=f(n+1)
E-1f(n)=f(n-1)
Master equation
Need to substitute into master equation and convert to equation for 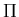 ,
sorting terms according to order in
,
sorting terms according to order in 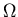 .
UGH!
Example:
MALTHUS-VERHULST PROBLEM
.
UGH!
Example:
MALTHUS-VERHULST PROBLEM
Birth and death problem in which
a logistic term to takes into account competition.
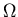 is the system size parameter.
is the system size parameter.
Birthrate:
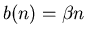
Death rate:
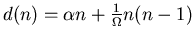 The Macroscopic rate equation is
The Macroscopic rate equation is
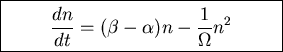
The steady state solutions are
n=0 , and
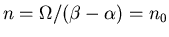
For
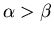 ,
n=0 solution is stable,
,
n=0 solution is stable,
n=n0 is unphysical. (Population dies out.)
For
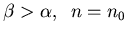 stable,
n=0 unstable.
stable,
n=0 unstable.
Population approaches carrying capacity.
Master equation is:
![\fbox{\parbox{13cm}{
\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\{(E...
...\alpha n +\frac{1}{\Omega}n(n-1)]+
(E^{-1}-1)\beta n\}P(n,t)\end{displaymath}}}](img27.gif)
Do our change of variable:
Substitute the expansions for E, E-1.
Find (after some algebra)
where
For the expansion in powers of 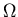 to work
must have
to work
must have ![$[\;]=0$](img31.gif) .
.
![$[\;]=0$](img31.gif) gives
gives
Equivalent to macroscopic rate equation!
(Remember
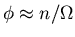 .)
.)
Solution
![\fbox{\parbox{8cm}{
\begin{displaymath}
\phi(t)=\frac{\phi(0)e^{(\beta-\alpha)t}}{1+\frac{\phi(0)}{\beta-\alpha}[e^{(\beta-\alpha)t}-1]}\end{displaymath}}}](img34.gif)
Solution depends only on net birth rate
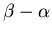 .
.
For
Will have to discuss the cases separately!
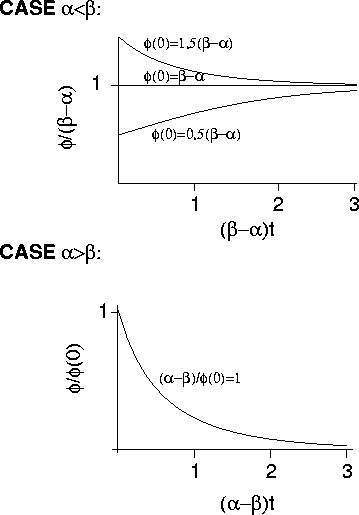
In general:
Require that terms of order
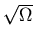 vanish.
Get for terms independent of
vanish.
Get for terms independent of 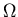
in system size expansion
FOKKER PLANCK EQUATION
For Malthus-Verhulst problem:
![\fbox{\parbox{14cm}{
\begin{displaymath}\frac{\partial\Pi(x,t)}{\partial t}=[\a...
...\alpha+\beta+\phi(t)]\phi\frac{\partial^2}{\partial x^2}\Pi\end{displaymath}
}}](img41.gif)
Substitute 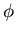 from solution to macroscopic equation.
from solution to macroscopic equation.
Can find results for mean and variance without solving
Fokker Planck equation:
Have
Integrate by parts
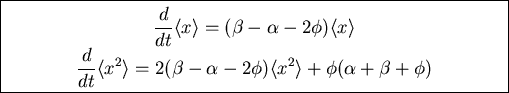
Interested in steady state fluctuations!
If
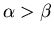 there is no steady state.
Population dies out!
there is no steady state.
Population dies out! 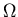 irrelevant!
THE CASE
irrelevant!
THE CASE
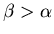
The population will now approach the macroscopic steady state
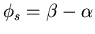
Assuming a
(t=0) fluctuation of size x0 i.e.
the solution is
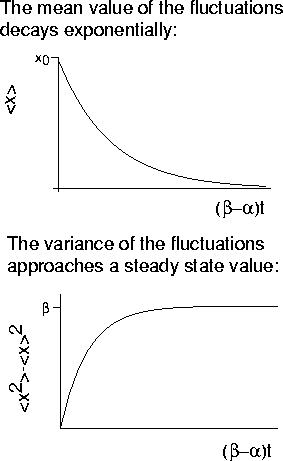
SUMMARY
- We analyzed a system in
terms of a macroscopic variable and fluctuations
- The master equation was expanded in powers of
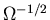 .
.
- Malthus-Verhulst problem used as an example.
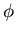 was found to satisfy a macroscopic
deterministic rate equation.
was found to satisfy a macroscopic
deterministic rate equation.
- Probability distribution of x satisfied a Fokker-Planck
equation.
- The mean and the variance of the fluctuations could be
extracted directly from the Fokker-Planck equation.
- While macroscopic equation only depended on effective birth rate
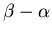 ,
fluctuations contained information about both.
,
fluctuations contained information about both.
Click here for 3. Fokker-Planck equation
Click here for Return to title page


Next: About this document ...
Birger Bergersen
1998-10-14
![\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\sum_{n'}[W(n\vert n')P(n',t)-W(n'\vert n)P(n,t)]\end{displaymath}](img1.gif)
![\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\sum_{n'}[W(n\vert n')P(n',t)-W(n'\vert n)P(n,t)]\end{displaymath}](img1.gif)
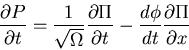
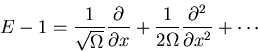
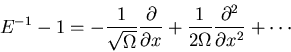
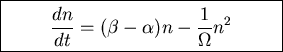
![\fbox{\parbox{13cm}{
\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\{(E...
...\alpha n +\frac{1}{\Omega}n(n-1)]+
(E^{-1}-1)\beta n\}P(n,t)\end{displaymath}}}](img27.gif)
![\fbox{\parbox{8cm}{
\begin{displaymath}
\phi(t)=\frac{\phi(0)e^{(\beta-\alpha)t}}{1+\frac{\phi(0)}{\beta-\alpha}[e^{(\beta-\alpha)t}-1]}\end{displaymath}}}](img34.gif)
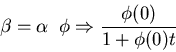

![\fbox{\parbox{14cm}{
\begin{displaymath}\frac{\partial\Pi(x,t)}{\partial t}=[\a...
...\alpha+\beta+\phi(t)]\phi\frac{\partial^2}{\partial x^2}\Pi\end{displaymath}
}}](img41.gif)