

Next: About this document ...
1. Master Equation
START WITH PHYSICAL PICTURE:
q= microscopic state of dynamic system
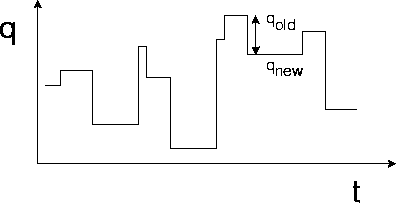
Changes by stochastic transitions
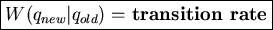
Rates
W(qnew|qold) for
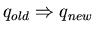 specify model.
specify model.
World of Fermi's golden rule.
In general microscopic fluctuations on timescales
short compared to times of interest.
Describe system by
P(q,t)
probability of state q at time t.
MASTER EQUATION
![\fbox{\parbox{11cm}{
\begin{displaymath}\frac{\partial P(q,t)}{\partial t}=\int dq'[W(q\vert q')P(q',t)-W(q'\vert q)P(q,t)]\end{displaymath}
}}](img4.gif)
- System changes by transitions in and out of states.
- Master equation describes evolution of the probability distribution
-not evolution of the state of the system.
- Assume system intrinsically stochastic.
SOME SPECIAL CASES
If state is integer n master equation discrete.
One step processes
Birth and death processes can be modeled as
taking place one at a time.
d=death rate.
b=birth rate.
Natural boundary
For birth and death processes: d(0)=0.
STEADY STATE
For all n.
For one step processes must have
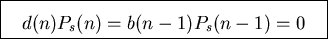
Express P(n) in terms of P(0).
Determine P(0) from normalization.
Boxed equation akin to detailed balance.
THERMODYNAMIC EQUILIBRIUM:
If steady state also equilibrium
(Click here
for tutorial on the Boltzmann equilibrium
concept),
require:
![\fbox{\parbox{11cm}{
\begin{displaymath}\frac{P_s(n')}{P_s(n)}=\frac{w_n'}{w_n}e^{-[U(n)-U(n')]/kT}=e^{-[F(n)-F(n')]/kT}\end{displaymath}
}}](img12.gif)
U(n)= internal energy state with n particles.
wn degeneracy factor (number of states with n individuals).
F=U-TS= free energy.
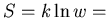 entropy.
entropy.
No restriction to one step processes!
We will later discuss detailed balance for microscopic processes.
Example:
INTRINSIC SEMICONDUCTOR
n=# of electrons=# of holes.
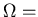 system size parameter = volume.
system size parameter = volume.
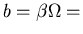 electron (hole) generation rate.
electron (hole) generation rate.
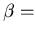 constant independent of volume.
constant independent of volume.
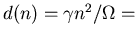 recombination rate.
recombination rate.
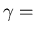 another constant independent of
another constant independent of 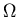 .
.
n=0=natural boundary, i.e. d(0)=0.
Macroscopic rate equation
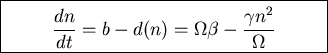
Expect mean number of carriers in steady state
Master equation for steady state
d(n)Ps(n)-bPs(n-1)=0
Substitute
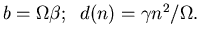 Express
P(1), P(2) etc. in terms of Ps(0).
Express
P(1), P(2) etc. in terms of Ps(0).
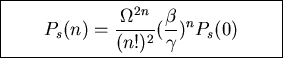
Solve for Ps(0) using the normalization condition
Use Stirling's formula
find that Ps(n) approximately Gaussian.
Mean and variance
At equilibrium
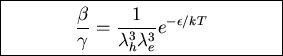
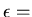 band gap,
band gap, 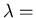 thermal wavelength
thermal wavelength
h= Planck const., k Boltzmann const.
m*= effective mass, T temperature.
Boltzmann/Gibbs formula
Z= normalizing factor (partition function).
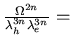 phase space factor.
phase space factor.
(n!)2= Gibbs factor for identical particles.
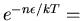 Boltzmann factor.
Boltzmann factor.
SUMMARY
- Master equation natural starting point when processes
intrinsically stochastic.
- Equation describes time evolution of probability distribution.
- When states discrete
![\fbox{\parbox{11cm}
{\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\sum_{n'}[W(n\vert n')P(n',t)-W(n'\vert n)P(n,t)]\end{displaymath}}}](img33.gif)
- Found exact steady state solution for one step processes
with a natural boundary.
- Rates restricted if required that steady state agrees with equilibrium Boltzmann-Gibbs
statistical physics.
- Mean agrees with rate equation result for large system.
Click here for 2. System size expansion
Click here for Return to title page


Next: About this document ...
Birger Bergersen
1998-09-18
![\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\sum_{n'}[W(n\vert n')P(n',t)-W(n'\vert n)P(n,t)]\end{displaymath}](img6.gif)

![\fbox{\parbox{11cm}{
\begin{displaymath}\frac{\partial P(q,t)}{\partial t}=\int dq'[W(q\vert q')P(q',t)-W(q'\vert q)P(q,t)]\end{displaymath}
}}](img4.gif)
![\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\sum_{n'}[W(n\vert n')P(n',t)-W(n'\vert n)P(n,t)]\end{displaymath}](img6.gif)
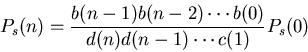
![\fbox{\parbox{11cm}{
\begin{displaymath}\frac{P_s(n')}{P_s(n)}=\frac{w_n'}{w_n}e^{-[U(n)-U(n')]/kT}=e^{-[F(n)-F(n')]/kT}\end{displaymath}
}}](img12.gif)
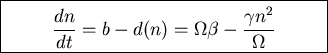
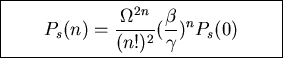
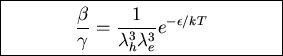
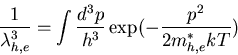
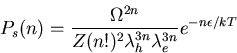
![\fbox{\parbox{11cm}
{\begin{displaymath}\frac{\partial P(n,t)}{\partial t}=\sum_{n'}[W(n\vert n')P(n',t)-W(n'\vert n)P(n,t)]\end{displaymath}}}](img33.gif)