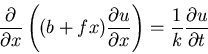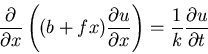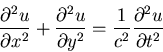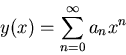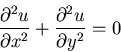

Next: About this document ...
PHYSICS 312
Sessional Examination,
April 1999
Answer 4 out of the 5 problems. All problems have equal
value. If all 5 problems are attempted credit will be given for the best 4 answers.
Problem 1:
Find the steady state solution of the problem
b,f,k are constants.
(This problem was given again as question 1 of midterm review problem set 2001.)).
Problem 2:
Find the six lowest frequencies of a vibrating membrame satisfying
The membrane is rectangular in shape with sides a and 2a, and u=0 on the boundary.
Problem 3:
The Laplacian in plane polar coordinates can be written
a:
Find a particular solution to
b:
Solve the boundary value problem
in the region
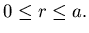
Problem 4:
The differential equation
is called Hermite's equation (
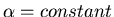 ).
).
a:
Find a recursion formula for the
coefficients an of the power series solution
subject to an initial condition
b:
For what initial conditions and values of 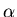 will
there be solutions to Hermite's equation that are polynomials
of order n
will
there be solutions to Hermite's equation that are polynomials
of order n
Show that the polynomial will contain either only odd or only even
power of n.
c:
Find polynomials of order n=3 and n=4 that are solutions to Hermite's
equation.
Problem 5:
Solve the boundary value problem
inside a square of side 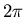 :
:
(This problem was given again as question 2 of midterm review problem set 2001.)).
END OF EXAMINATION
Return to title page.


Next: About this document ...
Birger Bergersen
2001-02-28