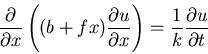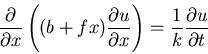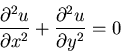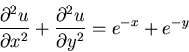

Next: About this document ...
PHYSICS 312
2001 Midterm review problem set
Problem 1:
Find the steady state solution of the problem
b,f,k are constants.
Problem 2:
Solve the boundary value problem
inside a square of side 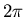 :
:
Problem 3:
In which of the following cases can solutions
be found by the method of separation of variables?
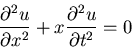 |
(1) |
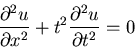 |
(2) |
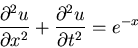 |
(3) |
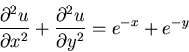 |
(4) |
In cases where the variables don't separate directly, transform
the equations so that product solutions can be found. You don't need to solve the resulting
ordinary differential equations.
Problem 4:
Show that the function
is an eigenfunction of the triangle T bounded by the lines
y=0,y=x,x=1 associated with
the differential equation
and the boundary condition
on the boundary of T. What is the eigenvalue 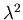 asociated with
asociated with 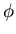 ?
?
Return to title page.


Next: About this document ...
Birger Bergersen
2001-02-28