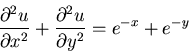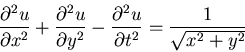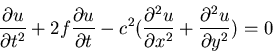

Next: About this document ...
PHYSICS 312
End of term review problem set 1999:
Problem 1:
In which of the following cases can solutions
be found by the method of separation of variables?
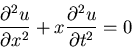 |
(1) |
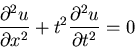 |
(2) |
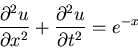 |
(3) |
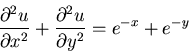 |
(4) |
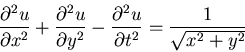 |
(5) |
In cases where the variables don't separate directly, transform
the equations so that product solutions can be found. You don't need to solve the resulting
ordinary differential equations.
(A modified version of this problem was given again as question 3 of midterm review problem set 2001.)
Problem 2:
The differential equation
(where p is a constant) is called Laguerre's equation.
- a:
- Find a power series solution of Laguerre's equation.
- b:
- When p is a positive integer or zero the power
series breaks off after a finite number of terms. If normalized so that
y(0)=p! the resulting polynomials are called Laguerre polynomials
Lp(x). Find
L0(x),L1(x) and L2(x).
Problem 3:
The concentration c of a certain chemical in a column of water
as a function of height z and time is given by
the diffusion equation
where D is the diffusivity. The boundary conditions
are
where h is the height of the water column.
The initial concentration is
- a:
- Find the steady state concentration.
- b:
- Find the concentration as a function of height and time.
- c:
- Find the time taken for the concentration at any point
to reach the mean of the initial and steady state values.
The trigonometric identity
may prove handy.
(This problem was given again as question 3 of problem set 4 2001.)
Problem 4:
A vibrating membrane is shaped in the form of a square of side
L and is weakly damped by frictional forces. Assume a
differential equation
where f and c are constants
- a
- Solve the differential equation using a Fourier expansion assuming as boundary condition
that the amplitude u is zero at the edges of the square and
that initially
where g(x,y) is a known function.
- b
- Will the modes of high frequency die out more rapidly
than the low frequency modes?
Return to title page.


Next: About this document ...
Birger Bergersen
2001-02-13