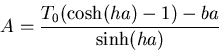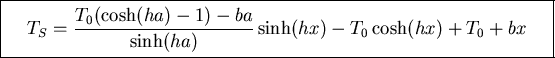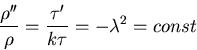

Next: About this document ...
PHYSICS 312,
Solution to Midterm Examination,
February 26 1999
Problem 1:
The steady
state temperature TS satisfies the
differential equation
With the boundary conditions
TS(0)=TS(a)=0
We introduce the new variable
u=TS-T0-bx
and substitute into the differential eqation to find
The general solution for u is
where A and B are constants to be determined. We find
The boundary condition at x=0 gives
B=-T0
The boundary condition at x=a gives
Giving
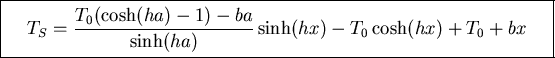
Problem 2:
In order to solve
we first solve the characteristic equation
giving the general solution to the differential equation
The boundary condition at x=0 gives B=0. The boundary
condition at 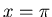 gives
gives
or
The three lowest eigenvalues and eigenfunctions are
You were only asked to give a sketch of the eigenfunctions.
A more accurate plot is given on the attached worksheet.
Problem 3:
a:
We attempt a separation of variables solution to
where without loss of genrality we can put c=1
The boundary condition at x=0 gives G=0.
The eigenvalue 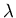 is now a continuous variable and
the eigenfunctions are on the form
is now a continuous variable and
the eigenfunctions are on the form
The coefficients
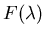 can be obtained from the Fourier sine
transform. We can thus write for the complete solution
can be obtained from the Fourier sine
transform. We can thus write for the complete solution
where
b:
In the
special case
where T0 is a constant,
the initial condition is already in the form of an eigenfunction with
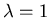 and we have the solution
and we have the solution
return to title page.


Next: About this document ...
Birger Bergersen
2000-02-03