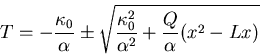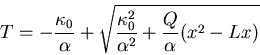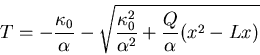

Next: About this document ...
PHYSICS 312.
Midterm Examination. February 27, 2000
SOLUTION
Problem 1 :
The function
g(x) in the range 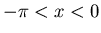 that constitutes the
that constitutes the
a: periodic extension of f(x) is
b: the odd periodic extension of f(x) is
c: the even periodic extension of f(x) is
Problem 2:
Let us define
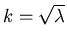 The general solution to
The general solution to
is
and
Hence B=-Ak and
The cosine term above vansihes and we get
or
The eigenfunctions can then be written
and the eigenvalues
Problem 3:
The steady state temperature differential equation is
The ends x=0 and x=L were kept at the temperature T=0
a: We integrate this equation to get
Integrating once more gives
The boundary condition T=0 at x=0 gives c=0 while
T=0 for x=L gives b=-QL/2. This gives us the quadratic equation
which can be solved for T to give for 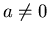
b: For 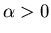 we must choose the positive root to get T=0 for x=0 and x=L. Hence
we must choose the positive root to get T=0 for x=0 and x=L. Hence
c: 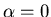 The division by
The division by 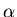 in the quadratic equation doesn't work and we
get instead
in the quadratic equation doesn't work and we
get instead
d: 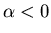 .
We must now pick the negative root in the solution to the quadratic
.
We must now pick the negative root in the solution to the quadratic
Bonus question:
If 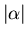 is too large and
is too large and 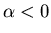 there
no longer is a real solution in the middle of the bar. The maximum value of x2-Lx occurs
for x=L/2 and is L2/4. Hence when
there
no longer is a real solution in the middle of the bar. The maximum value of x2-Lx occurs
for x=L/2 and is L2/4. Hence when
the calculation breaks down. What happens is that it gets so hot in the middle of the bar
that the thermal conductivity turns negative and we get a runaway solution with more and
more heat pouring in.


Next: About this document ...
Birger Bergersen
2001-02-16