

Next: About this document ...
PHYSICS 312.
Midterm Examination. February 27, 2000
Answer all three questions.
Problem 1 :
Consider the function
defined in the range 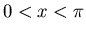 .
Find the function
g(x) that constitutes the
.
Find the function
g(x) that constitutes the
a: periodic extension of f(x).
b: odd periodic extension of f(x).
c: even periodic extension of f(x).
in the range 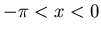
Problem 2:
Consider the following eigenvalue problem (assume
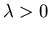 )
)
Normally boundary value conditions that involve combinations of the function and its derivatives lead to transcendental equations, but in this case the equations
can be solved explicitly.
Find the eigenvalues 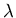 and eigenfunctions
and eigenfunctions 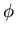 of the problem!
of the problem!
Problem 3:
Heat is produced uniformly inside a long thin bar at a constant rate per unit length.
Heat escapes from the ends but not from the sides of the bar.The thermal conductivity 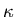 can in principle depend on the temperature T.
The steady state temperature inside the bar satisfies the differential equation
can in principle depend on the temperature T.
The steady state temperature inside the bar satisfies the differential equation
The ends x=0 and x=L are kept at the temperature T=0 and
a: When integrating the steady state differential equation you will
end up with a quadratic equation for T. Solve this equation to
find the steady state temperature distribution
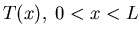 for
for
b: 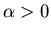
c: 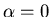
d: 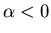
Bonus question:
In the last case (d:) you will find that if 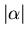 is too large there
no longer is a real solution in the middle of the bar. Can you explain
physically what goes wrong then?
is too large there
no longer is a real solution in the middle of the bar. Can you explain
physically what goes wrong then?


Next: About this document ...
Birger Bergersen
2000-03-05