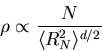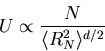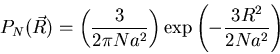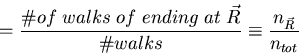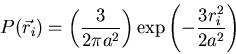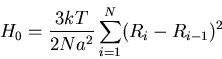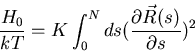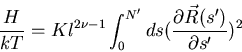

Next: About this document ...
18. Flory theory.Edwards model.
IN MY LAST LECTURE:
FLORY THEORY
Consider length R of chain as thermodynamic
variable which at equilibrium fluctuates about its most
probable value. This is somewhat analogous to how one
can treat magnetization M in the Heisenberg
or x-y models where in the ordered phase there are many
equivalent directions of M.
Recalling that the polymer is made up of N monomers
we find find for the density of monomers in a polymer environment:
Represent self-avoidance constraint by repulsive monomer-monomer interaction:
For a Gaussian walk the probability that chain has length 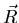 given by
given by
Rewrite as
Boltzmann entropy given by:
Hence
Free energy
Most likely value of R near minimum of F
or
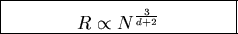
Obtain Flory formula
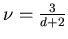 .
For
.
For
- d=1 we find
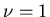 which is the exact value.
which is the exact value.
- d=2 we find
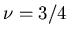 which is believed to be exact.
which is believed to be exact.
- d=3 Flory theory gives
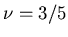 close to best estimate
close to best estimate
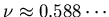 .
.
- d=4 find
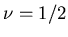 again exact.
again exact.
- d>4 find
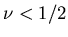 which is absurd. Interprete this by
saying self-avoidance "irrelevant" for d>4.
which is absurd. Interprete this by
saying self-avoidance "irrelevant" for d>4.
Flory theory example of "mean field theory" in the spirit of van der Waals
theory for gas liquid transition. Success of Flory theory due to cancellation of errors.
For further discussion see Bouchaud and Georges [1990].
EDWARDS MODEL
Go back to result for Gaussian chain
This result can be obtained by Gaussian model where
for each link in chain.
Express this in terms of Boltzmann factor
e-H0/kT where
This is the free energy of a set of coupled "springs" with
a spring constant proportional to the temperature.
This phenomenon called entropic elasticity.
In continuum limit:
Next take into account self-avoidance
constraint by including repulsion term
Provision should be made to exclude
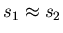 from region of integration (Oono [1985]). Ignore this problem here (but we
will come back to it later).
from region of integration (Oono [1985]). Ignore this problem here (but we
will come back to it later).
We write
H=H0+H1
for the free energy of the system.
We analyze the relative importance of the two terms by a
scaling argument:
The d-dimensional Dirac  function has the
scaling behavior
function has the
scaling behavior
Assume that lengths along the chain are rescaled according
to
N=l-1N'
We asume vectors R rescale as
so that
or
We note that H0 contains a scaling term
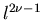 .
H1 scales as
.
H1 scales as
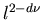 .
Then why is the Flory formula for the exponents not exact in
the Edwards model? The problem is that the region
|s1-s2|<a
should be excluded from the integral. The resulting correction
is not negligible, but it will in general scale differently
than the rest of the integral for H1. The problem is not
3-point and higher point interactions which could be added to the
expression for H1. It can be shhown that these shrink under
rescaling with l>1 when compared to the H1 term.
.
Then why is the Flory formula for the exponents not exact in
the Edwards model? The problem is that the region
|s1-s2|<a
should be excluded from the integral. The resulting correction
is not negligible, but it will in general scale differently
than the rest of the integral for H1. The problem is not
3-point and higher point interactions which could be added to the
expression for H1. It can be shhown that these shrink under
rescaling with l>1 when compared to the H1 term.
SUMMARY
- We have discussed self-avoiding random walk as example
of random process with long range correlations.
- Mean field model of Flory gave good agreement with
observed exponents
- Some insight into why Flory model works so well found
by studying Edwards model.
- Edwards model suitable starting point for renormalization group
analysis.
Return to title page


Next: About this document ...
Birger Bergersen
1998-12-03
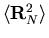 vs N.
vs N.
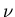 from fit of slope.
from fit of slope.