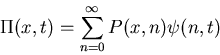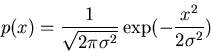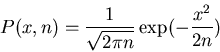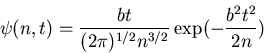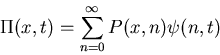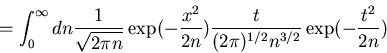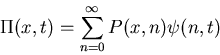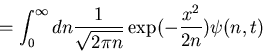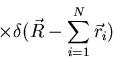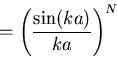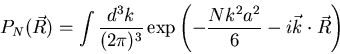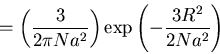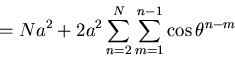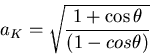

Next: About this document ...
15. Random walk in fractal time.
Correlated walks
LAST TIME
- Considered continuum time random walks in which
waiting time distribution were Lévy-stable.
- If the waiting distribution had no mean found
subdiffusion, i.e. typical excursion grew
slower than
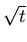 for large times.
for large times.
- Typical situations:
- Diffusion in lattices with traps.
- Diffusion in systems with many "blind alleys",
e.g. percolation clusters.
TODAY we will discuss:
- Random walks where the number
of jumps per unit time is Lévy stable.
- Associated phenomenon intermittency
- Near laminar flow
 turbulence transition typically have bursts of violent
activity followed by quiet periods.
turbulence transition typically have bursts of violent
activity followed by quiet periods.
- Similar behavior of fluctuations near first
order (discontinuous) phase transitions.
- In financial markets one observes periods with high
volatility and enormous trading volumes interspersed with
slow periods.
- We will also start discussing situation were jumps
are correlated.
INTERMITTENCY
Toy model for price fluctuations
Consider a market where
- x(t) represents
the change in price of a certain commodity
over a period of time t.
- where we work with changes in price, rather than price itself,
because we don't want to be bothered by having to make
prices positive definite.
- Each transaction leads to a small price change with
probability ditribution p(x).
- Assume these price changes uncorrelated.
- Probability after n transactions P(x,n).
- n= transaction volume governed by probability
distribution
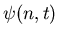 .
.
Probability distribution
for price change x after time t:
For simplicity assume Gaussian distribution for
the effect of a single transaction:
Without lack of generality we can choose our
unit price to be such that 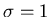 .
.
The price change distribution after n transactions is thus
We finally assume that the distribution for transaction volume is Lévy stable for large t:
As a first example let us assume transaction volume
follows Lévy-Smirnov
distribution:
Choose unit of time so that b=1!
Substituting we find
where we approximate n to be a continuous variable.
A change of variable
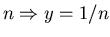 yields
yields
or
Price distribution Cauchy with 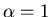 !
!
In the general case we note from
that
We find that
-
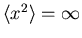 if
if 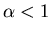
-
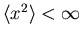 if
if 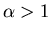
- From the central limit theorem we find that the prize
will undergo Brownian motion if
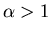 over a coarse
enough time scale.
over a coarse
enough time scale.
- Feller[1971] has shown that the distribution
 is Lévy stable with exponent
is Lévy stable with exponent 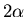 if
if 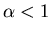 .
.
The rôle of "fractal time" distribution
of prizes in economics is discussed in detail in Mandelbrot[1997].
We next wish to consider "walks" were successive events are "correlated",
i.e. are not indenpendent of each other. In order to lay the groundwork
look at one more uncorrelated example:
FREELY JOINTED CHAIN
Consider a polymer such as
polyethylene which is a chain of molecules
Our discussion of the polymer problem be largely taken from chapter 8 of
Plischke and Bergersen [1994].
Let Ri be the position of the i-th carbon atom and
ri=Ri+1-Ri a vector representing the
i-th bond.
We first assume that the chain is freely
jointed i.e. each bond points in an arbitrary direction.
The probability that a N+1-carbon chain has an end to end
separation R is then
with a the length of the bond
Fourier transform:
For large N the function F(k) is sharply peaked at k=0:
and we see that for large N the freely jointed chain is
Gaussian
PERSISTENCE LENGTH
Polymers such as polyethylene are not freely
jointed. The angle between successive carbon carbon bonds is
fairly rigidly fixed at
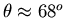
As our next approximation we put
where
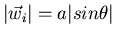 and
and
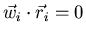 .
We assume that
.
We assume that
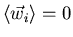
We find for the mean square displacement
After some manipulation of geometric series one finds
that the leading term of order N is
SHORT VS LONG RANGE CORRELATION
For the freely jointed chain
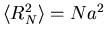 .
We conclude that the correlated random walk is still Gaussian,
but with an effective persistence length
.
We conclude that the correlated random walk is still Gaussian,
but with an effective persistence length
We can make the model more realistic by noting that the orientation of the vector wi is not uniformly distributed in the plane.
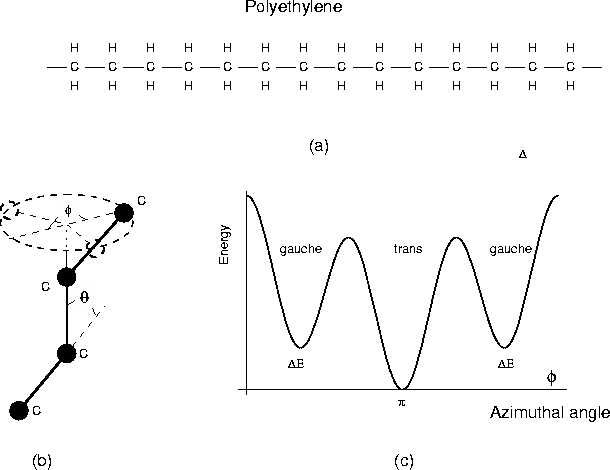
Instead wi will take into account one of three possible
directions (two "gauche" and one "trans").
This will not
change the fact that short range correlations will not affect the
Gaussian nature of the random walk - it will only modify
the value of the persitence length!
This picture changes when the correlations become long range!
THE SELFAVOIDING RANDOM WALK
If a polymer is disolved in a good solvent in a dilute solution it will
tend to "swell" i.e. occupy a larger volume than it otherwise would. In a "good solvent"
the only effective interaction between sections of the polymer is the excluded
volume effect - two segments of the polymer cannot occupy the same physical
space. In a dilute solution this excluded effect volume only acts on elements of
the same chain. The correlations introduced by the restriction of self-avoidance
will be long range and cannot be taken into account by introducing
a new effective persistence length!
Empirically on finds that the mean square end-to-end distance of
selfavoiding walks scales
as
where nu depends on the dimensionality d of the medium in which the
medium takes place, but is otherwise believed to universal i.e.
independent on the type of lattice, or if the walk is continuous or discrete.
In one dimension we must have 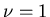 ,
the only possible self-avoiding walk is
one which continues in a straight line.
,
the only possible self-avoiding walk is
one which continues in a straight line.
For
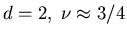 (this value is likely exact), while for
(this value is likely exact), while for
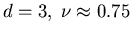 .
For
.
For
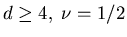 which is the same
value as we have for the Gaussian random walk. Hence, for
which is the same
value as we have for the Gaussian random walk. Hence, for 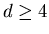 self-avoidance is irrelevant. Let us next review a few different
approaches to the problem of computing the scaling exponent
self-avoidance is irrelevant. Let us next review a few different
approaches to the problem of computing the scaling exponent 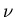 .
.
COUNTING WALKS
As an example consider the self-avoiding walks on a square lattice.
The simplest way to construct all N-step walks is to
proceed recursively-that is to add one step in all possible ways
to the N-1 step walk.
The self-avoiding walks up to order 3 on the square lattice are
listed below:
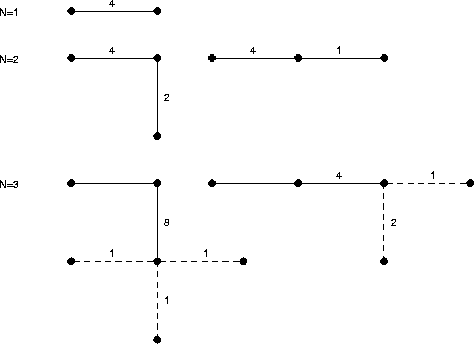
Next, we consider the walks of order 4 and 5:

The average end-to-end distance can then
be calculated from
Enumeration gives
The results are plotted in a log-log plot below
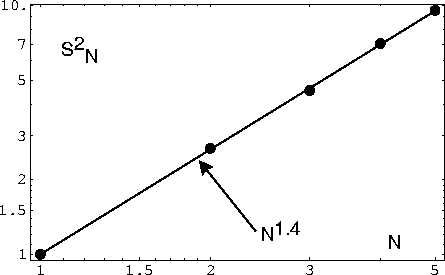
We find a good fit to
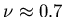 .
Clearly, more accurate results
can be obtained by goind to higher order- which is quite possible
with modern computers.
.
Clearly, more accurate results
can be obtained by goind to higher order- which is quite possible
with modern computers.
SUMMARY
- In previous lectures we showed that
- Random walk is
non-Gaussian if jump-distribution is Lévy-stable
with
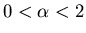 .
superdiffusion.
.
superdiffusion.
- Subdiffusion if waiting time distribution Lévy stable
with
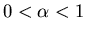 .
.
- Today showed Random walk Lévy -like with
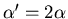 ,
if transaction rate
distribution is Lévy-stable with
,
if transaction rate
distribution is Lévy-stable with
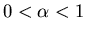
- Began to talk about correlated random walks.
- Showed that if correlations are short range the Gaussian
nature of walk prevails, with a different persistence length.
- Started to talk about the self-avoiding random walk.
Return to title page


Next: About this document ...
Birger Bergersen
1998-10-28