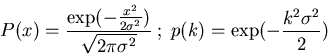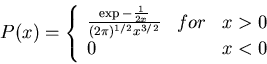

Next: About this document ...
11. Lévy-stable distributions
LAST TIME
- Rolf Luchsinger showed that Fokker-Planck (Langevin)
method helps us understand
molecular motors.
- There are a number of other important
applications
e.g. stochastic resonance.
- Need also to discuss limitations on
validity of approach :
- System size expansion
 Assume each
microscopic processes has little effect.
Assume each
microscopic processes has little effect.
 Rare events don't matter.
Rare events don't matter.
- Processes implicitly taken to be Markovian.
i.e. probability distribution for time-evolution of state
beyond t only depends on state of system at t.
- Today want to relax first assumption:
General reference Montroll and West [1987].
Much emphasis on Gaussian processes
- Fluctuations about stationary steady state
tend to exhibit Gaussian distribution!
- Central limit theorem
 Gaussian is "attractor" for random walk
when mean and variance of individual steps finite.
Gaussian is "attractor" for random walk
when mean and variance of individual steps finite.
- Probability for sum of two independent
Gaussian processes.
x=x1+x2
is Gaussian with
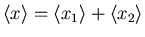 and
and
Augustin Cauchy and Paul Lévy asked:
What distributions share the property that
is of the same "type" as P1 and P2?
Non-Gaussian such distributions Lévy-stable.
Example:
CAUCHY DISTRIBUTION:
Using contour integration one finds that
i.e. the parameters a and b add under
convolution!
Cauchy distribution does not have a finite variance!
On the other hand derivation of Fokker-Planck equation from jump moments
assumed that in limit
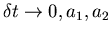 remain finite,
while
remain finite,
while
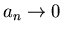 in limit.
in limit.
In probability theory Fourier transform of P(x) called
characteristic function
The last line follows from the properties of the Dirac
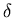 -function:
-function:
Not all functions p(k) can serve.
Normalization condition imposes constraint
p(0)=1
We must also have
Requirement that
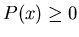 imposes further restrictions
on characteristic function.
imposes further restrictions
on characteristic function.
EXAMPLES:
Characteristic function of Gaussian
Cauchy distribution
p(k)=e-b|k|
Fourier transform of convolution integral
=p(k)=p1(k)p2(k)
Note that if
p1=p2=e-b'|k|
p(k) will be on the same form with b=2b'
b may be complex, as long as
p*(k)=p(-k) but we must have Re b>0
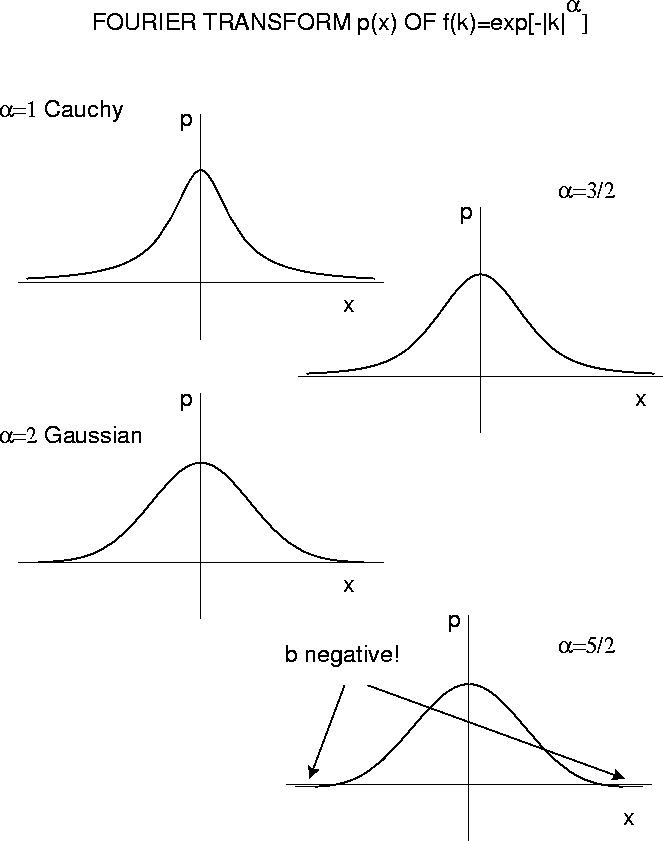
How does the Fourier transform of e-b|k| look?
Consider translationally invariant random walks
What is the most general form of P(x,t) that
is positive definite and normalized
and satisfies the chain condition
for all intermediate times t1?
A necessary and sufficient condition on P(x,t),
t>0
is that its characteristic function can be written
either on the form
with
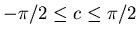 or
or
where v is real,
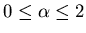 ,
,
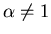 ,
b>0,
,
b>0,
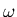 is real and
is real and
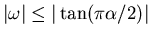 .
.
Theorem due to Khintchine and Lévy, proof in
Gnedenko and Kolmogorov [1954].
In most cases the inverse Fourier transforms cannot
be carried out analytically.
An interesting special case is
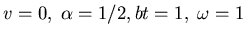 .
One finds
.
One finds
This function can be normalized, but has
neither mean nor variance.
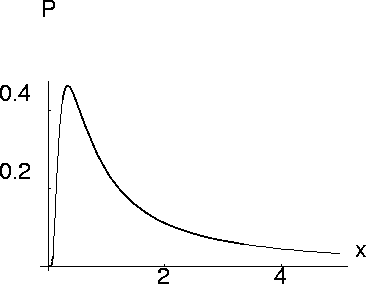
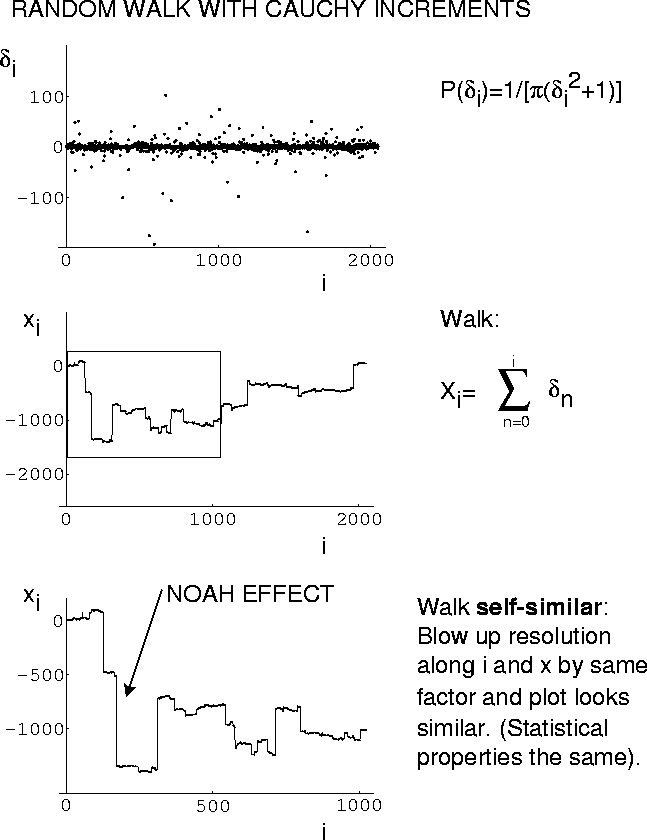
ASYMPTOTIC BEHAVIOR
Can show that inverse Fourier transform of
aproaches
if
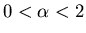
while cumulative distribution
(probability that 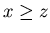 )
satisfies
)
satisfies
Power law implies scaling!
Rescale
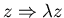 .
.
Rescale
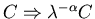
Power law distribution does not change!
SUMMARY
- Not all random walks approach a Gaussian distribution
- Chain condition
allow for Lévy distributions with
characteristic functions
"some restrictions apply".
- Asymptotically
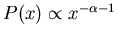
- Distributions have no variance if
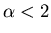 and
no mean if
and
no mean if 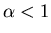 .
.
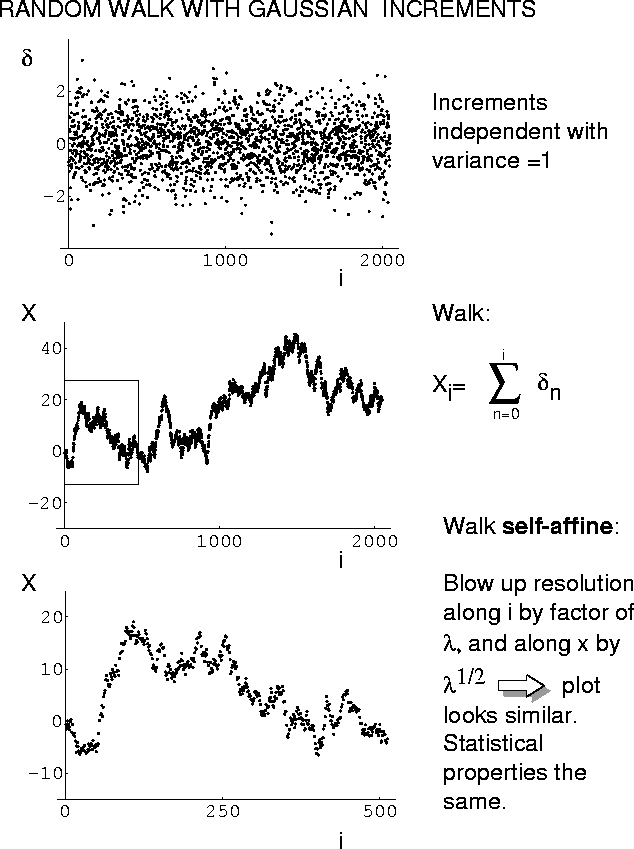
- Lévy walk self-affine.
- Lévy dust characterized by hierarchical arrangements of clusters
Return to title page


Next: About this document ...
Birger Bergersen
1998-10-14
 Assume each
microscopic processes has little effect.
Assume each
microscopic processes has little effect.
 Rare events don't matter.
Rare events don't matter.
![\begin{displaymath}P(x)=\frac{b}{\pi[(x-a)^2+b^2]}\end{displaymath}](img7.gif)
![\begin{displaymath}\frac{b_1+b_2}{\pi[(x-a_1-a_2)^2+(b_1+b_2)^2]}\end{displaymath}](img8.gif)
![\begin{displaymath}=\int_{-\infty}^{\infty}dx_1\frac{b_1b_2}
{\pi^2[(x_1-a_1)^2+b_1^2][(x-x_1-a_2)^2+b_2^2]}\end{displaymath}](img9.gif)