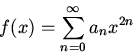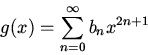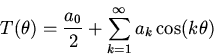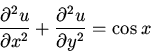Next: About this document ...
PHYSICS 312
Sessional Examination,
April 2000
Answer 4 out of the 5 problems. All problems have equal
value. If all 5 problems are attempted credit will be given for the best 4 answers.
Problem 1:
(Given again as question 2 of end of term problems set 2001)
The differential equation
is called the Chebychev equation.
a:
Show that the general solution to the equation can be written
where 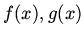 can be expanded in a power series containing only even or odd powers.
can be expanded in a power series containing only even or odd powers.
b:
For what values of the constant 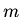 will the series for
will the series for 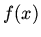 or
or 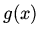 terminate
so that that the solution is a polynomial with a finite number of terms?
The resulting polynomials are called Chebychev polynomials
terminate
so that that the solution is a polynomial with a finite number of terms?
The resulting polynomials are called Chebychev polynomials 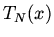 where
where 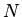 is the highest
power of
is the highest
power of 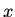 in the polynomial.
in the polynomial.
c:
The Chebychev polynomials are conventionally normalized so that
Find 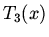 and
and 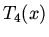 .
.
Problem 2:
(Given again as problem 2 of problem set 6 2001)
a:
For what values of the constants 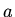 and
and 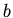 will
will
be a solution to the two dimensional heat equation
in polar coordinates.
b:
For what values of the constants 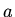 and
and 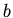 will
will
be a solution to the three dimensional heat equation
in spherical polar coordinates.
Problem 3:
(Given again as question 3 of end of term review problem set 2001)
a:
When separating variables in spherical coordinates we encountered the
differential equation
We transformed this equation into Legendre's equation by introducing the
new variable 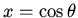 . An alternative approach is to assume
. An alternative approach is to assume
Use the trig identity
to find a recursion relation between 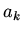 and
and 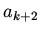 .
.
b:
For what values of the constant 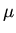 will the series for the even or odd coefficients break off after
a finite number of terms?
will the series for the even or odd coefficients break off after
a finite number of terms?
Problem 4
(Given again as question 4 of end of term review problem set 2001)
Solve
subject to the boundary conditions
Problem 5
(Given again as problem 3 of problem set 6 2001)
a:
Find solutions to the three dimensional wave equation
with no angular dependence satisfying the condition that 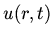 is finite at
is finite at 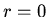 and
and
b:
Show that the three dimensional wave equation is satisfied
by
for arbitrary functions 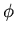 and
and 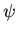 as long as they can be
differentiated twice with respect to their arguments.
as long as they can be
differentiated twice with respect to their arguments.
c:
What are the restrictions on 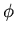 and
and 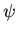 in part b:
for the solution to be bounded (
in part b:
for the solution to be bounded (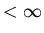 ) at the origin
) at the origin 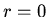 for all times.
for all times.
-------------------
The Laplacian in plane polar coordinates can be written
In three dimension the Laplacian in spherical coordinates simplifies to
if for some reason 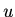 does not depend on the angles
does not depend on the angles 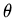 and
and 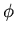 .
.
Return to title page.



Next: About this document ...
Birger Bergersen
2002-04-05