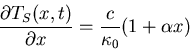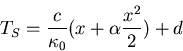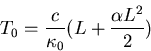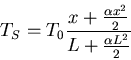

Next: About this document ...
PHYSICS 312.
Midterm Examination, March 2 2001, Solution
Problem 1 :
a:
Let us write
f(x)=f1(x)+f2(x)
is the periodic extension of f1(x) and also the even periodic extension.
Next
is the even periodic extension, but not the periodic extension of f2(x).
So statements 1 and 2 and 4 are false, while 3 is true!
b: Since we are dealing with the even periodic extension the Fourier series is a cosine series.
So statement 1 is truewhile 2 and 3 are false!
c: Calculate the coefficient 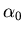 .
.
Problem 2:
By solving the characteristic equation
we find that the general solution to
is
if
and
for 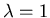 and
and
for 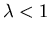 .
The boundary conditions were
.
The boundary conditions were
a: For 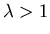 we have
we have 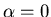 and
and
or
with eigenfunctions
b: For
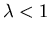 including
including 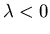 it is impossible to satisfy the boundary conditions.
The same holds for
it is impossible to satisfy the boundary conditions.
The same holds for 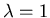 ,
so
,
so 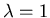 is not an eigenvalue.
is not an eigenvalue.
Problem 3:
The steady state solution satisfies
The boundary condition at x=0 gives d=0, while at the other end
so
Return to title page


Next: About this document ...
Birger Bergersen
2001-03-12