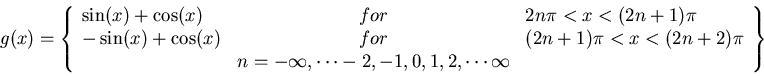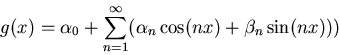

Next: About this document ...
PHYSICS 312.
Midterm Examination, March 2 2001
Answer all three questions. Allowed aids two sheets of formulas. Calculator.
Problem 1 :
Consider the functions
defined only in the restricted range 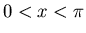 and
and
defined for all real x.
a: Which of the following statements are true
- 1.
- g(x) is the periodic extension of f(x).
- 2.
- g(x) is the odd periodic extension of f(x).
- 3.
- g(x) is the even periodic extension of f(x).
- 4.
- none of the above.
Justify your answer.
We make a Fourier expansion of the function g(x)
b: Which of the following are true
- 1.
- all the coefficients
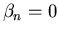 .
.
- 2.
- the coefficients
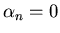 for n>1.
for n>1.
- 3.
- none of the above.
c: Calculate the coefficient 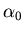 .
.
Problem 2:
Consider the following eigenvalue problem
a: Find the eigenvalues and eigenfuntions for 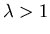 .
.
b: Are there any eigenvalues for 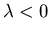 ? for
? for
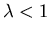 ?
Is
?
Is 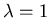 an eigenvalue?
an eigenvalue?
Problem 3:
Consider the heat conduction problem
The ends x=0 and x=L are kept at the temperatures T=0 and T=T0, respectively, and
the thermal conductivy depends on the position
Find the steady state temperature TS.
END OF EXAMINATION
Return to title page


Next: About this document ...
Birger Bergersen
2001-03-12