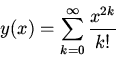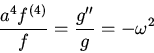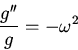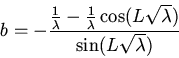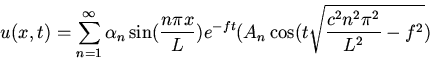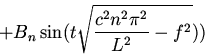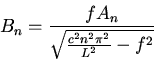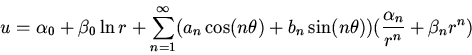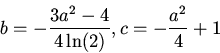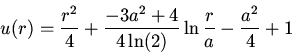Next: About this document ...
PHYSICS 312
Sessional Examination,
April 2002, Solution
Problem 1:
Substituting
into the differential equation
gives
Substituting 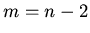 in the first term and
in the first term and 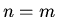 in the second gives
in the second gives
a:
If
the power series will only contain even terms. With
We find
b:
We recognize this power series as that of
We have
We find by substitution that the differential equation is satisfied.
c:
>From a: we have
The boundary condition require 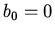 ,
, 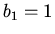 hence
hence
Problem 2:
a:
Substituting
into the fourth order differential equation
gives the characteristic equation
with roots
or
an alternative form which is a bit more convenient for the remainder of the
problem is
b:With
we find
We identify 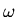 as the frequency of vibration and obtain
as the frequency of vibration and obtain
giving the modes
c:
If the end at 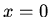 is clamped down we must have
is clamped down we must have
The conditions at the other end then yield
This gives rise to a determinantal equation for the frequencies 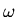
You were not asked to go beyond this point, but if we multiply out we find
using
This is a transcendental equation which can be solved numerically.
Problem 3:
a:
Substituting
into
gives the differential equation for 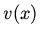
b: The general solution to this equation can be written
In order to satisfy the boundary condition at 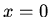 we
must put
we
must put
The boundary condition at the other end then gives
This will work for almost all values of 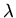 . If by accident
. If by accident
some special attention has to be paid.
c:
We can solve the boundary value problem
by writing
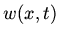 will then have to satisfy
will then have to satisfy
with boundary condition
where 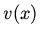 was found above. This problem can be solved
by separation of variables and expanding the initial condition
in a Fourier sine series in the usual way.
was found above. This problem can be solved
by separation of variables and expanding the initial condition
in a Fourier sine series in the usual way.
Problem 4:
Substituting
a:
into
gives
The solution to the differential equation for 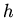 is with the
boundary condition that
is with the
boundary condition that 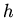 is zero at
is zero at 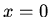 and
and 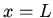
The differential equation for 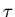
has solutions
giving
We expand the initial condition 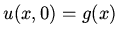 in a sine series and find
in a sine series and find
The condition
Gives
where 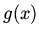 is a known function.
is a known function.
b:Since the damping term 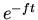 is independent of the mode number
is independent of the mode number 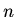 all the modes die out at the same rate
all the modes die out at the same rate
c: The maximum value of the damping constant for oscillations
to occur at the n'th frequencies is
As the damping is increased the lower frequency modes become over-damped
before the high frequency modes.
Problem 5
The general solution to the 2-dimensional Laplace equation in polar coordinates
is
a:
The solution to
in the region 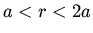 with
with
will be on the form
We have
we find
b:
The solution is now on the form
we find
giving
c:The solution will depend on 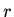 only. We rewrite the differential equation as
only. We rewrite the differential equation as
giving
Integrating once more gives
With the boundary conditions
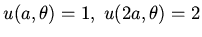 we find
we find
with solution
and we find



Next: About this document ...
Birger Bergersen
2003-04-09
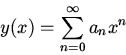
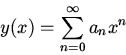
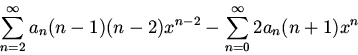
![\begin{displaymath}\sum_{m=0}^\infty x^m[(m+2)(m+1)a_{m+2}-2(m+1)a_m]=0\end{displaymath}](img6.gif)