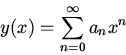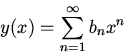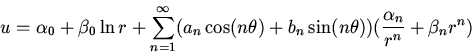Next: About this document ...
PHYSICS 312
Sessional Examination,
April 2002
Answer part a: of 4 out of the 5 questions and parts b: and c: of
3 questions. If more problems are attempted credit will be given for the best answers in each class. Allowed aids: Up to 4 sheets of formulas. Calculator.
Problem 1:
Consider the differential equation
a:
Find a solution 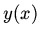 with the initial condition
with the initial condition
as a power series
b:
Do you recognize this power series as that of a familiar function?
What is it? Substitute into the differential equation and verify that you have the
correct solution.
c:
Find a second solution with the initial condition
in terms of a power series
Problem 2:
a:
Find the general solution to the fourth order differential equation
b:
The transverse vibrations of a thick rod can be shown to satisfy the fourth
order partial differential equation
Find solutions on the separated variable form for the vibrations.
c:
If the ends are clamped down both 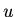 and
and
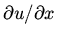 vanish.
Find an equation that the frequencies of vibration must
satisfy for a
rod of length
vanish.
Find an equation that the frequencies of vibration must
satisfy for a
rod of length 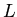 with both ends clamped down.
(you are not required to actually solve the equation).
Problem 3:
with both ends clamped down.
(you are not required to actually solve the equation).
Problem 3:
When studying radioactive decay one may encounter the heat equation on the form
where
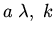 are constants, and the inhomogeneous term on the right
hand side comes from heat produced by the decaying atoms. For
simplicity let us assume that
are constants, and the inhomogeneous term on the right
hand side comes from heat produced by the decaying atoms. For
simplicity let us assume that 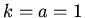 and that
and that 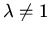
a:
Attempt a particular solution
and find a differential equation that 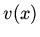 must satisfy.
must satisfy.
b:
Solve the differential equation for 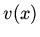 subject to the boundary
value condition
subject to the boundary
value condition
c:
Discuss how you would solve the boundary value problem
where 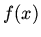 is a given function.
is a given function.
Problem 4:
A vibrating string of length
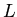 is weakly damped by drag forces. Assume a
differential equation
is weakly damped by drag forces. Assume a
differential equation
where 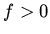 and
and 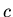 are constants.
are constants.
a:
Solve the differential equation using the separation variables method assuming as boundary condition
that the amplitude 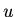 is zero at
is zero at 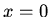 and
and 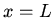 and
that initially
and
that initially
where 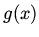 is a known function.
is a known function.
b: Will the modes of high frequency die out more rapidly
than the low frequency modes?
c: What is the maximum value of the damping constant for oscillations
to occur at the different frequencies.
Problem 5
The general solution to the 2-dimensional Laplace equation
in polar coordinates is
Find the solution to the Laplace equation in polar coordinates
in the region 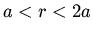 if
if
a:
b:
c:Find the solution to
in the region 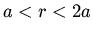 if
if
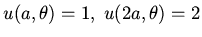



Next: About this document ...
Birger Bergersen
2002-04-18