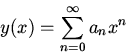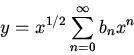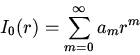Next: About this document ...
PHYSICS 312
Sessional Examination,
April 2001
Answer part a: of 4 out of the 5 questions and parts b: and c: of
3 questions. If more problems are attempted credit will be given for the best answers in each class. Allowed aids: 4 sheets of formulas. Calculator.
Problem 1:
(Given again as question 1 of problem set 6 2002.)
Consider the differential equation
a:
Find a solution 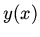 with the boundary condition
with the boundary condition 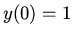 as a power series
as a power series
b:
Do you recognize this power series as that of a familiar function?
What is it?
c:
Show that the differential equation also admits a solution
by finding a recursion relation for the coefficients 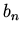
Problem 2:
(A modified version is given again as problem 1 of problem set 4 2002.)
Two identical metal bars are each of length a. Initially one is at temperature 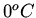 while the other is at temperature
while the other is at temperature 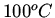 . They are joined together
end to end and the assembly thermally isolated. Assume the temperature satisfies the heat equation
. They are joined together
end to end and the assembly thermally isolated. Assume the temperature satisfies the heat equation
with boundary conditions
a:
Find the steady state solution and formulate the boundary value problem for the transient.
b:
Find the transient
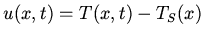 in the form of a Fourier series.
in the form of a Fourier series.
c:
Evaluate the Fourier coefficients of the transient.
Problem 3:
(A modified version was given again as question 1 of problem set 5 2002.)
The Laplacian in spherical coordinates can be written
if for some reason 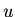 does not depend on the angles
does not depend on the angles 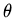 and
and 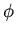 .
Assume that
.
Assume that 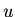 is independent of the angles
and solve
is independent of the angles
and solve
with the boundary condition
a:
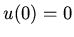
b:
and 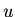 bounded for
bounded for 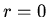 .
.
c:
Problem 4
(Given again as question 2 of problem set 6 2002.)
A compact way of representing the Legendre polynomials is by Rodriguez formula
To make this result plausible
a:
compute
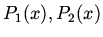 and
and 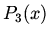 using the formula
using the formula
b:
verify that 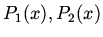 and
and 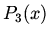 computed above satisfies
computed above satisfies
c:
Show that 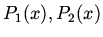 and
and 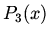 computed above satisfies Legendre's differential
equation
computed above satisfies Legendre's differential
equation
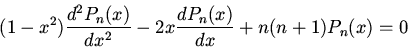 |
(1) |
for the appropriate 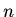 .
.
Problem 5
(Given again as question 3 of problem set 6 2002.)
When considering heat flow around a flat circular disk with convection one encounters
the modified Bessel equation of order zero.
The solutions to this equation, that are bounded at the origin, are called modified Bessel functions of order 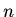 and written
and written 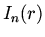 . In this problem we restrict our attention to the case
. In this problem we restrict our attention to the case 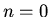
a: Assume that 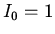 and make a power
series expansion
and make a power
series expansion
Find a recursion formula relating 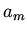 to
to 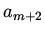
b: Find 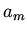 for
for 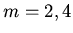
c: Show that 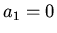 if the solution is bounded for
if the solution is bounded for 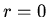 .
.
END OF EXAMINATION
Return to title page.



Next: About this document ...
Birger Bergersen
2002-04-05