


Next: About this document ...
PHYSICS 313
Second midterm 2000.
Problem 1:
The multiplicity of an Einstein solid with 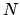 oscillators and
oscillators and 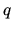 vibrational quanta is
vibrational quanta is
a:
Show using Stirlings formula
that when 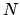 is large the entropy of the Einstein solid can be written
is large the entropy of the Einstein solid can be written
b:
The internal energy is
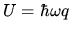 , where
, where 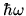 is the energy of a single quantum. Use the
thermodynamic identity
is the energy of a single quantum. Use the
thermodynamic identity
to find the temperature 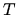 and chemical potential/oscillator
and chemical potential/oscillator
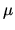 , as a function of
, as a function of 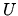 and
and 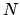 .
.
c:
Evaluate the entropy per particle (in natural units)
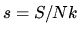 at the "Einstein temperature"
at the "Einstein temperature"
Problem 2:
One container contains 2 mol of helium while another contains 1 mol of oxygen.
Initially both gases have temperature 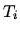 and volume
and volume 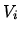 . Assume the gases are ideal.
. Assume the gases are ideal.
a:
The partition between the two containers is broken so that they spontaneously mix with a total volume 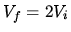 . How does the entropy of the system change?
. How does the entropy of the system change?
b:
The mixture is compressed isothermally until the volume is 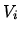 . How much work has to
be done on the gas? What happens to the entropy of the system?
. How much work has to
be done on the gas? What happens to the entropy of the system?
c:
Answer question a: if both containers initially contain helium.
The entropy of an ideal gas can be written
where the entropy per molecule 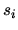 due to internal degrees of freedom such as vibration and rotation and the quantum volume
due to internal degrees of freedom such as vibration and rotation and the quantum volume 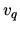 depends only on the temperature and not on the volume
depends only on the temperature and not on the volume 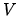 or number of
particles
or number of
particles 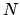 .
.



Next: About this document ...
Birger Bergersen
2001-10-02