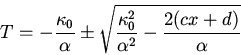Next: About this document ...
PHYSICS 312.
Midterm. February 10 2003.Solution.
Problem 1:
a:
We have
Integrating the last equation we find
where  is a constant. Solving for
is a constant. Solving for  and
and 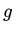 gives
gives
Adding the terms gives
b: This is a bell shaped pulse moving left, without changing its shape from its initial form.
Problem 2:
a:We have
The boundary condition for 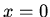 gives
gives 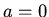 . The
boundary condition at
. The
boundary condition at 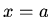 gives
gives
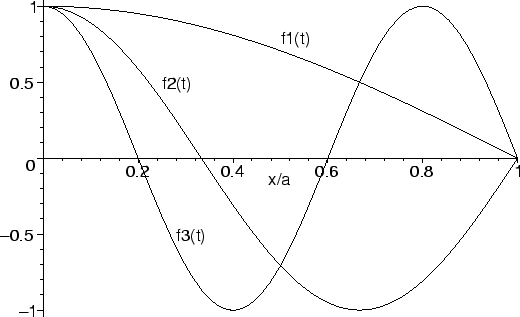
b: The three lowest eigenfunctions can be written
drawn below. The constant 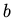 is arbitrary and we choose it to be unity.
Problem 3:
is arbitrary and we choose it to be unity.
Problem 3:
a: We have
Choosing the constant to be 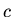 and integrating once more
gives
and integrating once more
gives
where 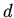 is another constant.
is another constant.
b: The solution to the equation above is
The boundary condition at 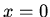 forces us to choose the positive root and put
forces us to choose the positive root and put
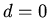 . The boundary condition at
. The boundary condition at 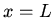 gives
gives
or
c: We must use the positive root.



Next: About this document ...
Birger Bergersen
2003-02-24