

Next: About this document ...
PHYSICS 312
1999 Midterm eview problem set:
Problem 1: In a heat conduction problem the steady
state temperature TS satisfies the
differential equation
with boundary conditions
TS(0)=TS(a)=0
find TS.
This problem was assigned again as problem 1 of Problem set 2, year 2000,
for solution click here.
Problem 2: At Watson Lake in Yukon the average temperature through the year is -2oC. The average daily temperature reaches a maximum of
14oC in July 15. Assume that the average daily temperature varies
sinusoidally through the year.
- a:
- Obtain an expression for the temperature as a function of time and distance below the ground surface.
- b:
- At what depth will the ground be permanently frozen. Assume one year is
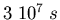 ,
and that the constant k in the heat equation is
,
and that the constant k in the heat equation is
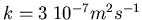 a
a
Problem 3:
- a:
- For which values of
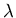 will
will
have solutions satisfying
- b:
- Find the eigenfunctions
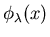
This problem was assigned again as problem 1 of Problem set 3, year 2000,
for solution click here.
Problem 4:
- a:
- Find the solution to the wave equation
satisfying
Hint: try solutions on the form
f(x+ct)+g(x-ct)
- b:
- Sketch the solutions for times
This problem was assigned again as problem 2 of Problem set 3, year 2000,
for solution click here.
Problem 5:
Can you find functions
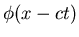 that satisfy
the one dimensional heat equation
that satisfy
the one dimensional heat equation
i.e. can you find traveling wave solutions to the heat equation?
Can such a solution be realized physically?
Return to title page.


Next: About this document ...
Birger Bergersen
2000-03-20