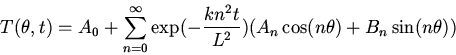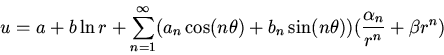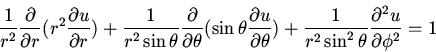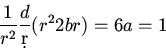Next: About this document ...
PHYSICS 312
Solution to problem set 5 1999:
Problem 1:
a:
If 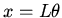 represents distances along the perimeter of the ring the
differential equation is
represents distances along the perimeter of the ring the
differential equation is
In terms of the angle 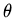 the differential equation becomes
the differential equation becomes
Separating the variables
we find
The general solution to the equation for 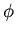 is
is
If the angle is incremented by 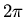 we are back were we started,
hence
we are back were we started,
hence 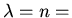 integer or zero. The solution for
integer or zero. The solution for 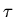 is
is
The solution to the problem can thus be expressed on the
Fourier series form
where
b
In this case 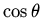 is an eigenfunction with eigenvalue
is an eigenfunction with eigenvalue 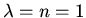 Hence we put
Hence we put 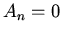 for
for 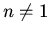 and
and 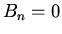 for all
for all 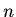
The time it takes for the temperature difference between the hottest
and coldest spot to halve is thus
Problem 2:
The general solution to the 2-dimensional Laplace equation
in polar coordinates is
Because of the
boundary conditions
only the cosine term with 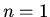 will contribute to the solution so we can write
will contribute to the solution so we can write
Substituting for the conditions at 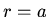 and
and 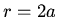 we
find
we
find
we find
and
Problem 3:
The differential equation
becomes in spherical coordinates
The boundary conditions are such that 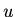 does not depend on either
does not depend on either
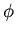 nor
nor 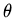 . The differential equation then simplifies to
. The differential equation then simplifies to
The general solution to the homogeneous equation
is
where 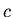 and
and 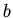 are constants. We require that
are constants. We require that 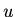 is bounded
at
is bounded
at 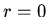 hence
hence 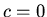 . We must add to the homogeneous solution a particular solution to the inhomogeneous
equation. It was suggested to try a solution on the form
. We must add to the homogeneous solution a particular solution to the inhomogeneous
equation. It was suggested to try a solution on the form
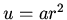 . Substituting into the differential equation
gives
. Substituting into the differential equation
gives
Giving 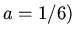 The boundary condition
The boundary condition
gives 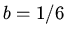 Hence
Hence
Return to title page.



Next: About this document ...
Birger Bergersen
2002-04-18