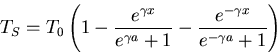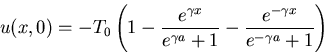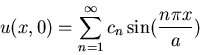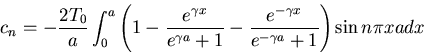

Next: About this document ...
PHYSICS 312
Problem set 3 1999:
Solution
a:
The general solution to
is
The boundary conditions TS=0 for x=0 and x=a
allow us to solve for A and B to obtain
b:
Substituting
u=T-TS
into
gives
c:
The initial temperature distribution for u is
d:
The initial temperature distribution can be written on the
form
where
We can solve the time dependent problem formally by
assuming that the Fourier coefficients are time dependent
i.e.
where 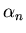 satisfies the initial condition
satisfies the initial condition
Substituting into the partial differential equation
gives
with solution
e:
In order to use the method of separation of variables
the partial differential equations must be homogeneous.
This is necessary in order to use the superposition principle.
It might be tempting to make the
equation homogeneous by the substitution
u=T-T0
We then get the homogeneous problem
with initial condition
u(x,0)=-T0
If we apply the method of separation of varables
we will not get the correct solution!. The
problem is that the method of separation of variables
method give particular solutions to the partial
differential equation. To these we should in principle
add a time-independent solution to
The appropriate solution to use is the steady state temperature. Only when we subtract this temperature,
are we guaranteed that the particular solution is the complete solution.
For part f: see Maple worksheet.
Return to title page.


Next: About this document ...
Birger Bergersen
2000-02-21