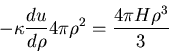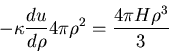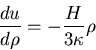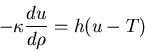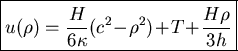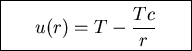

Next: About this document ...
PHYSICS 312
SOLUTION TO PROBLEM SET 2 1999:
Problem 1:
In the steady state heat flows radially at the same rate
as it is generated. The heat balance condition at radius
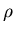 is
is
which simplifies to the first order differential equation
with solution
where a is aa constant to be determined. The boundary
condition at the surface 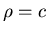 is
is
We find
and
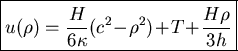
Problem 2:
The condition that the heat flow is constant can be written
We call this constant
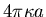 giving
the differential equation
giving
the differential equation
with solution
The boundary conditions give b=T, a=-Tc and
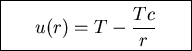
Note that the solution is independent of 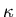 !
!
For problem 3: see attached Maple worksheet.
Return to title page.
Birger Bergersen
2000-02-21