PHYSICS 312
End of term projects:
Solve 1 of the following problems:
(more problems may be added to list)
Due last day of classes:

Problem 1:
a: Solve Laplace's equation

$$\nabla^2u(x,y)=0$$

inside a square of side a with boundary conditions

$$u(0,y)=u(a,y)=\sin(\frac{\pi y}{a})$$

$$u(x,0)=u(x,a)=\sin(\frac{\pi x}{a})$$

Hint: It is convenient to break the problem into two subproblems:

u=u₁+u₂

where u₁ and u₂ both satisfy the Laplace equation but with different boundary conditions.

$$u_1(0,y)=u_1(a,y)=\sin(\frac{\pi y}{a})$$

u₁(x,0)=u₁(x,a)=0

u₂(0,y)=u₂(a,y)=0

$$u_2(x,0)=u_2(x,a)=\sin(\frac{\pi x}{a})$$

b:
Plot the solution found under a: assuming a=6

c:
Solve the problem numerically using the method of finite differences, using a grid of 25 internal points. Note that because of the symmetry of the problem only six of the interior points and three of the exterior points are different as seen in the grid below

$$\begin{array}{ccccccc} &a&b&c&b&a&\\ a&1&2&3&2&1&a\\ b&2... ...b&2&4&5&4&2&b\\ a&1&2&3&2&1&a\\ &a&b&c&b&a&\\ \end{array}$$

d:
Compute for comparison the exact solution for the six inequivalent interior points.

Problem 2:
A spherical object is initially at temperature T₀. It is put in convective contact with a heat bath a temperature 0. In the long time 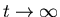$t\rightarrow\infty$ limit the sphere will thus reach temperature 0. By symmetry the temperature inside will depend only on the radial coordinate r and t. The boundary condition at r=a is that

$$\frac{\partial T(r,t)}{\partial r}=-hT(r,t)$$

The heat equation is

$$\nabla^2T=\frac{1}{k}\frac{\partial T}{\partial t}$$

a: Solve the problem formally using the methods of separation of variables.
b: Solve the problem numerically and plot the radial temperature distribution for some typical temperatures. Put a=k=h/2=T₀=1.
c: How long will it take for the temperature to reach T₀/2 at the center.

Problem 3:
Solve the roast cooking problem of lecture 22 assuming convective boundary conditions (as in problem 2).

Return to title page.