


Next: About this document ...
PHYSICS 312
Problem set 4:
Problem 1:
Give a physical interpretation for this problem and thus explain why 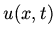 should increase steadily as
should increase steadily as 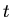 increases.
(Assume that
increases.
(Assume that 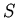 is a positive constant).
is a positive constant).
Problem 2:
Show that
satisfies the heat equations and boundary conditions in the problem above. Find 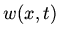 defined by
defined by
Problem 3:
Show that the four functions
are solutions to the heat equation. (These are sometimes called heat polynomials.) Find a linear combination of them
that satisfies the boundary conditions
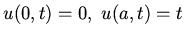 .
.
Return to title page.
Birger Bergersen
2003-01-30