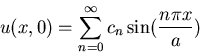

Next: About this document ...
PHYSICS 312
Problem set 3:
A rod of length a is initially (t=0) at temperature
T=0. It is put into convective contact with a fluid
with temperature T0. The temperatures
at the ends (x=0) and (x=a) are kept at T=0, but
towards the middle the temperature rises towards T0.
Assume that the temperature distribution satisfies
the differential equation
for t>0, with k and 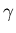 constants.
constants.
a:
Find the steady state temperature distribution TS(x).
b:
Find the differential equation satisfied by the transient.
u(x,t)=T(x,t)-TS(x)
c:
What is the initial temperature distribution
for the transient?
d:
Solve the transient problem formally, by assuming
that the initial temperature u(x,0) has a
Fourier sine series:
(for this part of the problem you don't need to calculate the
Fourier coefficients).
e:
Could you find the time dependent temperature distribution
directly without subtracting the steady state?
f:
Plot the temperature distribution at time t=1
for
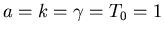 .
(For this part of the problem
you need to compute the first few Fourier coefficients
either with or without the steady state subtracted.)
Return to title page.
.
(For this part of the problem
you need to compute the first few Fourier coefficients
either with or without the steady state subtracted.)
Return to title page.
Birger Bergersen
2000-01-23